논리 게이트는 입력과 출력 사이의 특정 논리적 관계를 따르는 전자 회로입니다. 즉, 입력의 특성에 따라 출력의 존재에 관한 논리적 결정을 내립니다.
영어 수학자 인 George Boolean (1815-1864)은 논리의 수학적 분석을 다루기위한 특정 대수 작전을 개발했습니다. 부울 대수라고합니다. 이 논리에는 주로‘높음’또는‘낮음’의 두 값 만 포함됩니다. ‘폐쇄’또는‘열기’; ‘켜짐’또는‘꺼짐’; ‘참’또는‘거짓’등은 각각 1과 0입니다.
따라서 변수에 대해 부울 대수를 통해 두 개의 상태 나 값 만 표시 될 수 있습니다. 이 두 값 또는 상태는 세 가지 작업을 포함하는 부울 대수를 나타냅니다. 그들은 부름을받습니다. 이것들은 a, b 등으로 표시되는 입력 간의 관계이며 출력은 Y로 표시됩니다.
작동하지 않음
작업은 갱단 스위치로 표시 될 수 없습니다. 스위치 a가 닫히면 B가 자동으로 열리고 그 반대로.
작업은 다음 표에 표시 될 수 있습니다.

부울 대수에서 NOT 작동은 주로 변수의 막대 또는 대시로 표시됩니다. 따라서 부울 발현은
에 의해 주어진다y =a '
위의 부울 표현은 y가 A가 아니라고 구두로 표현된다. 입력 A가 존재하고 그 반대의 경우 출력 y가 존재하지 않는다고 명시한다.
게이트가 아닌 의미
출력이 입력과 동일하지 않은 디지털 전자 장치는 게이트가 아닙니다. 따라서 GATE NOT GATE에는 하나의 입력이 있으며이 입력은 하나의 출력으로 반전됩니다. NOT GATE에는 입력 데이터가 포함 된 두 개의 터미널이 있고 다른 하나는 출력이 생성됩니다. 입력은 a로 표시되고 Y에 의해 출력 될 수 있습니다.
기하학적 기호 :
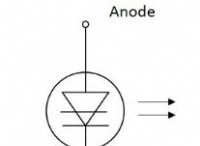
회로 다이어그램에서 Not Gate는 아래 그림과 같이 표시됩니다.

위의 그림에서, 삼각형의 오른쪽 끝에있는 기포를 반전 거품이라고합니다.
부울 표현 :
부울 대수의 관점에서, Not Gate의 작동은 다음과 같이 표시됩니다.

그것은 y가 아닌 것을 암시했다.
진실 테이블 :
진실 테이블은 입력의 모든 관련 조합과 해당 출력을 보여주는 테이블로 정의됩니다. 진리 테이블을 만들려면 이진 숫자 1과 0을 사용해야합니다. a =1은 A를 입력 한 것을 나타내며 y =1은 출력 y가 존재 함을 시사합니다. 존재는 1 이상으로 지정 될 수 있으며, 존재하지 않는 것은 0 또는 OFF로 표시 될 수 있습니다.
입력과 해당 출력의 게이트 조합이 아닌 진리 테이블에 표시 될 수 있습니다.

게이트 실현이 아닌 회로
트랜지스터 증폭기에서 입력 신호가 반전되므로 이러한 이유로 인해 다이오드 대신 공통 이미 터 구성이 트랜지스터 증폭기에 사용됩니다. 따라서이 구성으로 인해 신호의 위상이 변경됩니다.
게이트가 아닌 디지털 회로는 다음과 같습니다.

위의 회로에서 두 가지 일반적인 경우가 발생할 수 있습니다.
- a =0 :A가 배터리의 접지 터미널에 연결되면 접합이 바이어스 될 때 에이터베이스 접합을 통해 흐르는 수집기 전류가 없습니다. 트랜지스터 전위가 차단되기 때문에 r₁에 걸친 전위 감소는 0으로 감소합니다. 따라서 C에서의 배터리 전압과 출력 단자 (y)의 전압은 동일하거나 동일합니다. 즉 +5 V입니다. 따라서 y =1.
- a =1 :A =1 :A가 배터리의 +5 V 단자에 연결되면, 접합이 전방 바이어스 될 때 많은 양의 수집기 전류가 r₁을 통한 이미 터베이스 접합부에서 흐릅니다. 따라서, C에서 배터리 전압 및 RAL을 가로 지르는 전압 강하는 트랜지스터가 포화 상태에있는 것과 동일합니다. 또한, 수집기 C는 전도체 트랜지스터를 통해 접지 될 것이다. 따라서 y =0.
결론
Not Gate는 하나의 입력 만 허용 할 수 있고 하나의 출력 만 제공하는 논리 게이트입니다. 따라서 GATE NOT GATE에는 하나의 입력이 있으며이 입력은 하나의 출력으로 반전됩니다. NAND 나 등과 같은 다른 유용한 게이트를 만드는 데 사용되는 기본 게이트입니다. 또한 사각형 웨이브 발진기도 생성합니다. 다이오드뿐만 아니라 범용 게이트를 사용하여 구현할 수 있습니다. NOT GATE의 IC 번호는 7404입니다.