인덕턴스 L과 저항 R이 직렬로 연결되면 회로를 LR 회로 또는 LR 필터라고합니다. 그들이 직렬로 연결되어 있기 때문에, 둘 다 동일한 양의 전류가 그들을 통해 흐를 것입니다.
LR 회로의 개별 요소
조합 회로로 점프하기 전에 개별 요소를 빠르게 살펴 보겠습니다.
-
저항 만 AC 소스에 연결되면 공식 i =iosinwt로 표시되는 전위와 전위가 v =vosinwt이므로 전류 방정식은 다음과 같습니다.
i =vo/r
-
인덕터 만 AC 소스에 연결된 경우, 전류는 분류 I =iosin (wt-π/2)으로 표시되는 900에 의한 전위를 차지하고 전압은 V =vosin (wt)이므로 전류에 대한 방정식은 i =v0/xl xl이된다.
xl =2πfl이고 그 장치는 옴 (ω)
-
Capacitors 만 AC 소스에 연결되면 전류는 900에 의해 전위를 이끌며, 이는 공식 i =iosin (wt+ π/2)으로 표시되고 전압은 v =vosin (wt)이므로 전류에 대한 방정식은 i =v0/xc가됩니다.
xc =1/ 2πfc이고 그 단위는 옴 (ω)
LR 회로
직렬 LR 회로에서 저항 및 인덕턴스는 AC 소스에 직렬로 연결됩니다.
여기서, 저항에 들어가기 전에 회로를 통해 흐르는 전류는 i =i0sinwt.
입니다.전류가 저항에 들어가면 저항 VR의 전위차와 인덕터 VL의 전위차는 시간이 지남에 따라
로 표시됩니다.vr (t) =(v0) r 전류에 따라 Sinwt는 저항의 잠재력으로 위상이므로
및
vl (t) =(v0) l sin (wt+π/2) 인덕터에서와 같이 현재는 900
에 의해 전위가 지연됩니다.여기서 (v0) l은 인덕턴스의 전위의 피크 값이고 (v0) r은 저항의 전위의 피크 값입니다.
여기, v0은 다음과 같이 계산할 수 있습니다.
(v0) 2 =(v0) r2 + (v0) l2
(v0) =√ ((v0) r2 + (v0) l2)
이것은 직렬 회로이므로 저항을 통한 전류와 인덕턴스는 동일합니다. 따라서
i0 =il =ir
(v0) =√ (i02r2 + i02xl2)
(v0) =√ (i02 (r2 + xl2))
(v0) =i0 √ (r2 + xl2)
여기 √ (r2 + xl2)는 일종의 저항이므로
(v0) =i0z
여기서 z는 회로의 임피던스로 알려져 있습니다.
따라서, 임피던스는 일련의 RL 회로에서 전류의 흐름을 반대하는 저항 R과 인덕턴스 L의 집단 저항이다.
Phasor 다이어그램에 따르면, 전류는 여전히 RL 회로의 전위를 뒤흔들고 있지만 순수한 인덕터 회로에서와 같이 90 °는 아닙니다. 0에서 90 ° 사이입니다. 이 각도는 φ입니다.
φ 값은 Phasor 다이어그램에서 쉽게 찾을 수 있습니다 :
tanφ =xl / r
AC 의전력 계수
일반적으로 전력 p는
로 계산됩니다p =vi
그러나 AC 회로에서는 전압 v와 전류 모두 시간에 따라 다릅니다. 따라서 다음과 같이 순간 전력 p (t)를 계산합니다.
p (t) =v (t) i (t)
또는
p (t) =v0sinwt i0 (sinwt + ф)
rl 회로는 항상 전류가 전위를 뒤덮고 다음과 같은 간단한 공식을 사용하여 전력 계수를 계산하는 회로입니다.
cosф =r/z
LR 회로 예제
예 1 :
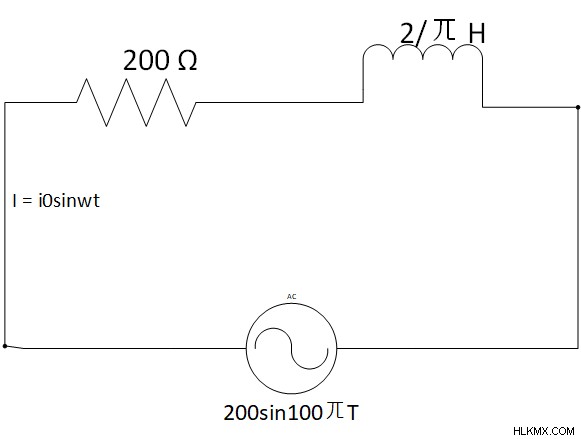이 회로는 다음을 찾으십시오.
-
귀납적 원자로 xl
-
임피던스 z
-
피크 전류 i0
-
i (t)
솔루션 :
유도 리액턴스 xl
xl =wl =100 ㄫ x 2/ㄫ =200 ω
임피던스 z
z =√ (r2 + xl2) =√ ((200) 2 + (200) 2 =200√2 ω
피크 전류 i0
i0, =v0/z =200/200√2 =1/√2 a
i (t) =i0sin (100 ㄫ t-φ)
tanφ =xl/r =200/200 =1
φ =450
따라서
i (t) =1/√2 sin (100 ㄫ t- ㄫ/4)
예제 2 :
다음 회로를 고려하십시오 :
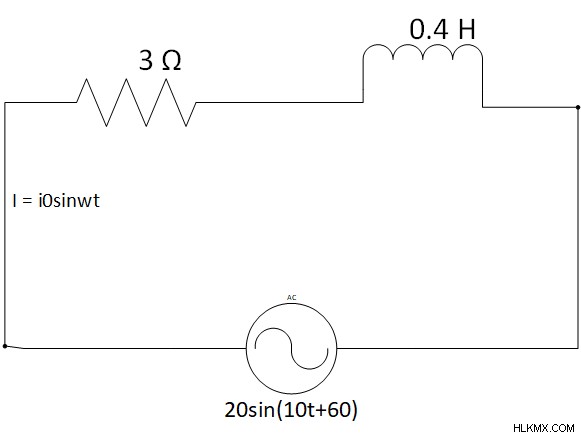
찾기
- xl
- z
- i0
- i (t)
- vr (t)
- vl (t)
솔루션 :
- xl =wl =10 * 0.4 =4Ω
- z =√ (r2 + xl2) =√ (42 + 32) =5Ω
- i0 =v0/z =20/5 =4a
- 먼저이 φ의 값을 계산하자
tanφ =xl/r =4/3
φ =530
i (t) =i0sin (10t + 600-φ)
i (t) =4sin (10t +600-530)
i (t) =4sin (10t + 70)
vr (t) =(v0) r sin (10t + 70)
(v0) r =i0r
=4 x 3
=12
vr (t) =12 sin (10t + 70)
vl (t) =(v0) l sin (10t + 70 + 900)
(v0) l =i0xl
=4 x 4
=16
vl (t) =16 sin (10t + 970)
결론
간단한 공식과 정의의 도움으로 LR 회로를 쉽게 해결할 수 있습니다. LR 회로의 임피던스는 전위로부터 전류의 총 지연을 결정하는 데 중요한 역할을합니다. 전력 계수, ф, W와 같은 다양한 측면은 LR 필터의 효율적인 기능을 위해 함께 작동합니다.
