중심 힘 아래로 움직이는 신체의 면적 속도가 일정하는 이유는 다음과 같습니다.
1. 각 운동량의 보존
* 중심 힘은 항상 고정 지점 (힘의 중심)을 향한 힘입니다. 이것은 힘이 몸을 중심에 연결하는 반경 벡터에 수직 인 성분이 없음을 의미합니다.
* 외부 토크가 없으면 각 운동량이 보존됩니다.
* 중심 힘의 경우 힘의 중심에 대한 토크는 힘이 방사형이기 때문에 0입니다. 따라서 신체의 각 운동량이 보존됩니다.
2. 각 운동량과 뇌 속도와 관련이 있습니다
* 질량체 (m)의 각 운동량 (m)의 힘 중심에서 속도 (v)로 움직이는 각 운동량 (m)은 다음과 같이 주어진다. l =mvr sin θ, 여기서 θ는 속도와 반경 벡터 사이의 각도이다.
* 작은 시간 간격 (DT)으로 신체에 의해 휩쓸린 영역은 반경 벡터와 변위 벡터 (V DT)에 의해 형성된 평행 사변형 영역의 약 절반입니다.
*이 영역은 다음과 같습니다. da =(1/2) r (v dt sin θ)
* 따라서, areal 속도 (da/dt)는 :da/dt =(1/2) rv sin θ입니다.
3. 도트 연결
* 각 운동량과 면적 속도에 대한 표현을 비교하면 다음을 볼 수 있습니다.
* l =2m (da/dt)
* 각 운동량 (L)이 보존되기 때문에, 면적 속도 (da/dt)도 일정하다.
간단한 용어로 :
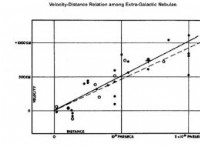
* 별을 공전하는 행성을 상상해보십시오. 별의 중력이 중심이기 때문에 행성의 각 운동량은 일정합니다.
*이 일정한 각도 운동량은 행성이 동일한 시간에 동등한 영역을 휩쓸어 일정한 면적 속도를 초래한다는 것을 의미합니다.
참고 : 면적 속도는 스칼라 양 (크기 만 있음)이며 항상 양수입니다.
이 원칙은 행성, 위성 및 중앙 세력 아래에서 움직이는 다른 물체의 움직임을 이해하는 데 중요한 영향을 미칩니다.