전자 스핀은 Zeeman 효과에 기여하며, 이는 성간 공간에서 자기장을 연구하고 별 형성을 예측하는 데 사용됩니다.
전자 라는 단어를들을 때 , 아마도 떠오르는 것은 아마도 매우 작고 부정적인 하전 된 구체, 요소의 전자 구성 및 전류가 전자의 흐름에 기인한다는 사실 일 것입니다. 그러나, 청구되고 움직이고, 그들은 또한 자극성 특성을 가지고 있으며, 이는 양자 척도에서 상당히 흥미로운 현상을 일으키며, 심지어 성간 척도에서도 결과를 초래합니다.
.자기에 기여하는 전자의 고유 특성을 스핀 이라고합니다. . 거시적 척도에서 스핀의 영향을 이해하려면 먼저 스핀이 무엇인지 이해하는 것이 중요합니다.
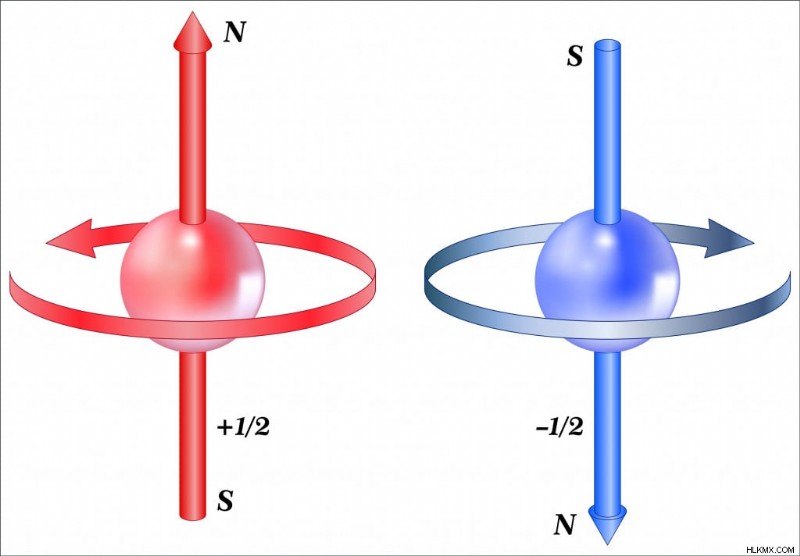
전자는 회전 구인 것처럼 행동하여 자기장의 생산을 초래합니다. (사진 크레딧 :Fouad A. Saad/Shutterstock)
전자 스핀 :Misnomer
Bohr의 원자 이론은 양자 세계에 대한 고전 이론의 확장이었다. 본질적으로, 전자는 지구가 태양을 공전하는 것처럼 핵을 공전하는 것으로 가정했다. 따라서, Sun-earth 시스템의 전체 수학적 프레임 워크 (각 운동량, 각속 속도, 회전 및 혁명의 에너지 등)는 전자-핵 시스템으로 확장되었습니다.
전자는 공간 질량 분포가없는 포인트 전하로 작동하기 때문에 , 고전적인 역학의 회전 비유는 폐기되었고 궤도 비유 (즉, 핵에 대한 혁명) 만 유지되었다. 따라서, 전자는 궤도 각 운동량을 가지고 있다고 가정되었다. 및 관련 궤도 자기 모멘트 .
나중에 실험은 전자가 고유 자기 모멘트와 고유 각 운동량을 갖는 것으로 나타 났으며, 이는 궤도 성분과 독립적 인 고유 각 운동량을 가지고 있음을 보여 주었다.
이것은 세례 스핀 각 운동량 입니다 및 스핀 자기 모멘트 고전적인 관점에서 생각할 때 의미가 있었기 때문입니다. 전자는 회전하지 않습니다 때문입니다 그것은 특별한 상대성의 법칙을 어 기게 될 것입니다 . 따라서 스핀은 잘못된 이름이므로 물체의 물리적 회전과 혼동해서는 안됩니다.
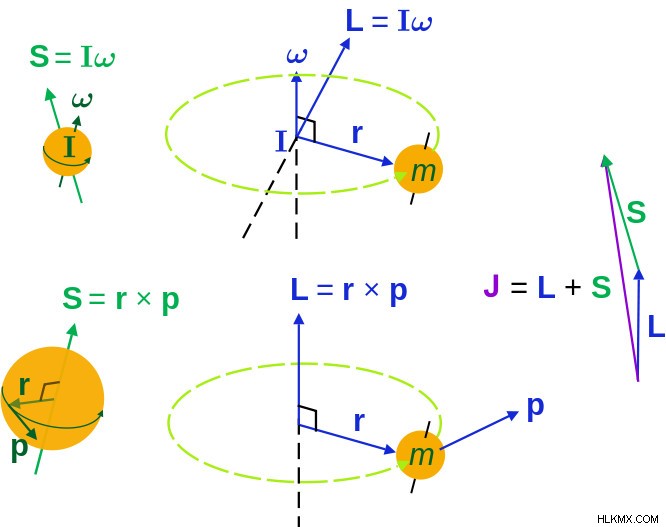
L은 궤도 각 운동량이고 S는 스핀 각 운동량입니다. J는 L과 S의 벡터 합인 총 각도 운동량입니다 (사진 크레디트 :Maschen/Wikimedia Commons)
전자 스핀의 효과 :Zeeman Effect
수소 원자를 고려하십시오. Bohr는 전자가 취할 수있는 특정 궤도 만 있다고 가정했습니다. 그것들을 고정 상태라고 불렸다 . 이것을 대표하는 편리한 방법은 Principal Quantum 번호 n, 를 사용하는 것입니다. 여기서 n 궤도 번호를 나타냅니다. 예를 들어, n =1 가장 낮은 궤도 (핵에 가장 가깝고 가장 안정적인), n =2 였습니다. 다음으로 허용되는 궤도는 n =1 보다 높은 에너지였습니다. . 마찬가지로, 추가의 궤도는 n =3, 4, 5, 로 지정되었다 … 등. n 의 값이 클수록 , 전자 에너지가 클수록.
nth 궤도는 :
에 의해 제공됩니다
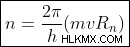, 여기서
h =Planck 's Constant,
m =전자의 질량,
v =전자의 궤도 운동의 선형 속도,
r =nth 궤도의 반경
전자에 에너지를 제공하면 이들을 더 높은 에너지 상태로 촉진합니다 ( n =1 n =2, 3, 4 , …, 등.). 에너지가 풍성한 전자가지면 상태로 되돌아 가면, 두 주요 양자 상태의 에너지 차이와 동일한 에너지로 전자기 방사선을 방출합니다. 이러한 전환은 분광계를 통해 볼 수 있습니다 및 스펙트럼을 방출 스펙트럼이라고합니다 .
수소 원자의 방출 스펙트럼. 스펙트럼 아래의 척도는 발생 위치를 측정하며, 이는 전이의 파장을 나타냅니다. (사진 크레디트 :Patrick Edwin Mora/Wikimedia Commons)
외부 자기장의 존재하에 수소의 방출 스펙트럼이 분석 될 때, 이상한 현상이 발생한다. Bohr의 이론은 n =3 의 선을 트리플렛으로 분할하는 것을 올바르게 예측했습니다. n =2 궤도 각 운동량을 고려한 전환 . 그러나 나트륨의 스펙트럼을 분석 할 때, n =3 ~ n =2 와 같은 다양한 전이에 해당하는 라인 또는 n =4 ~ n =3 은 3 줄 이상으로 나뉩니다 Bohr의 이론에 의해 예측되었습니다.
그것은 스핀 자기 모멘트라고 불리는 고유 자기 모멘트의 존재에 의해서만 설명 될 수 있었다. . 이 스핀 자기 모멘트는 궤도 자기 모멘트와 상호 작용합니다 다중 밀접한 간격의 선을 생성합니다.
수학적으로 궤도 및 스핀 자기 모멘트는 다음과 같이 제공됩니다.
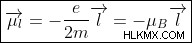및 
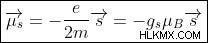
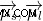=스핀 자기 모멘트 및 궤도 자기 모멘트,
e =전자 충전
m =전자의 질량.
, 
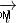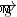=궤도 각 운동량 및 스핀 각 운동량,
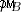=bohr magneton,
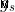=Lande 's Spin G-Factor ~ 2.002
이 두 사람이 추가되면 결과 자기 모멘트는
에 의해 제공됩니다.
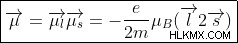
이 자기 모멘트는 Zeeman Effect 을 담당합니다 . 외부 자기장의 존재하에 라인의 분할은 주파수 변화도 발생한다는 것을 의미합니다. 주파수 이동은 다음과 같습니다.
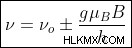여기서
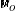=변속 주파수
g =Lande의 G-Factor
b =자기장 강도
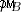= bohr magneton
h =Planck 's constant
상기 방정식에서 b 주파수가 알려진 경우 계산할 수 있습니다. 이 주파수는 분광계를 사용하여 측정됩니다.
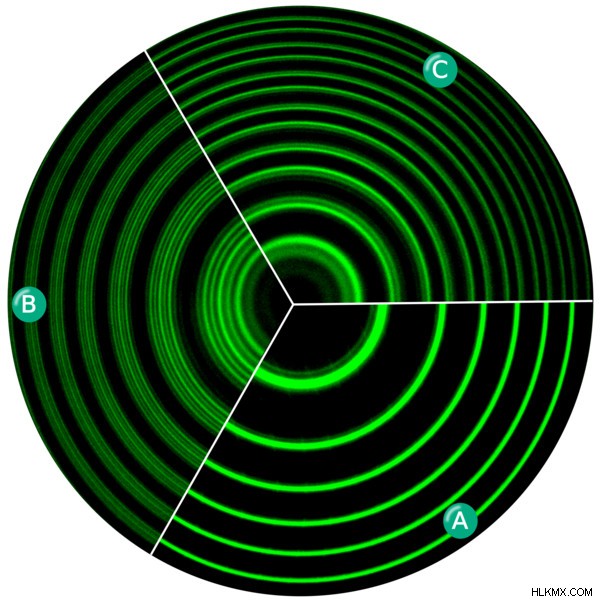
수은 증기의 스펙트럼 라인. A는 자기장이 없습니다. B는 자기장이 횡 방향 제만 효과를 생성하고 C는 세로 제만 효과를 보여줍니다. (사진 크레디트 :Warren Leywon/Wikimedia Commons)
where,m =가스 구름의 질량
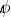=자기 플럭스
g =보편적 중력 상수 ~ 6.674 
10-11 m3/kg/s2
이것은 이론적 임계 비율입니다 중력 풀이 자기 힘에 의해 균형을 이루는 계산에 따라.
스펙트럼 관측
이 공간 영역으로부터의 방출 스펙트럼이 분석되고 자기장의 실제 강도 b 다음 방정식을 사용하여 계산됩니다.
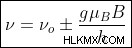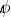. 계산됩니다.
가스 구름의 질량이 관찰됩니다 (이 과정은이 기사의 범위를 벗어납니다) 및 관찰 된 (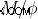 
) o 비율이 계산됩니다.
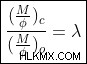
성간 공간에서의 별 형성은 자기장과 중력 인력 사이의 상호 작용에 의해 결정됩니다. (사진 크레딧 :antares_starexplorer/shutterstock)
케이스 I :만약에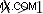 
, 클라우드 질량은 supermarical 입니다. 그리고 자기장은 질량의 중력 붕괴를 그 자체로 멈출 수 없어서 잠재적 인 별 형성을 초래합니다.
사례 II :만약에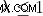 
, 자기장만으로는 가스 구름이 중력 붕괴에서 멈출 수 있습니다.
최종 단어
전자는 그들과 관련된 2 개의 자기 모멘트, 궤도 자기 모멘트 및 스핀 자기 모멘트를 갖는다. 이 모멘트의 상호 작용은 외부 자기장의 존재 하에서 에너지 수준의 분할을 야기합니다.
성간 공간에는 약한 자기장이 포함되어 있습니다. 관심 영역이 관찰되면, 방출 스펙트럼은 또한 분할 에너지 수준에 해당하는 미세한 선을 포함합니다. 그런 다음 주어진 공간 영역에서 자기장을 계산하는 데 사용됩니다.
이런 식으로, 양자 현상은 거시 스케일 효과를 관찰하는 데 사용될 수 있습니다!
