동역학 분자 가스의 이론 ( kmt 또는 단순히 가스의 동역학 이론 )는 통계 역학을 사용하여 가스의 거시적 특성을 설명하는 이론적 모델입니다. 이러한 특성에는 가스의 압력, 부피 및 온도가 점도, 열전도율 및 질량 확산 성을 포함합니다. 기본적으로 이상적인 가스 법칙의 적응이지만, 동역학 분자 가스 이론은 정상적인 조건에서 대부분의 실제 가스의 거동을 예측하므로 실제 적용이 있습니다. 이론은 물리 화학, 열역학, 통계 역학 및 공학에 사용된다는 것을 발견합니다.
동역학 분자 가스 가정 이론
이론은 가스 입자의 본질과 행동에 대한 가정을 만듭니다. 본질적으로 이러한 가정은 가스가 이상적인 가스로 작동한다는 것입니다 :
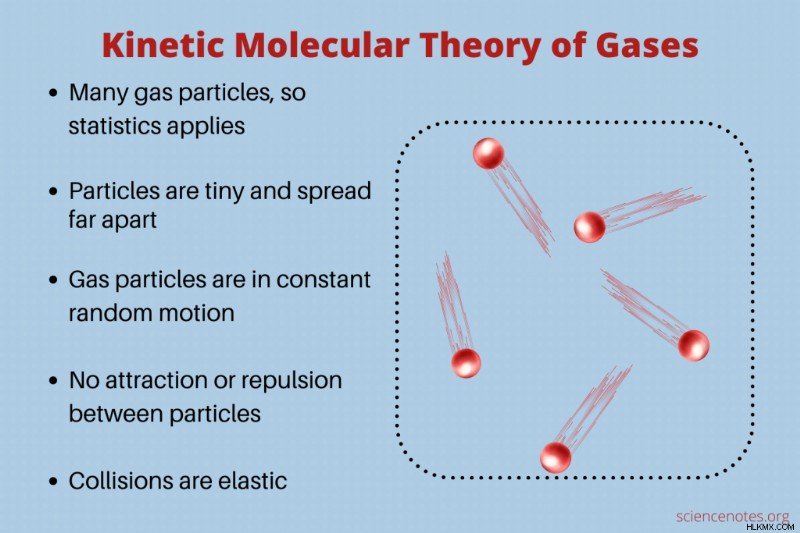
- 가스에는 많은 입자가 포함되어 있으므로 통계를 적용하는 데 유효합니다.
- 각 입자는 무시할만한 부피를 가지고 있으며 이웃과 먼 거리에 있습니다. 다시 말해, 각 입자는 점 질량입니다. 가스의 볼륨은 대부분 빈 공간입니다.
- 입자는 상호 작용하지 않습니다. 즉, 그들은 서로에 끌리거나 격퇴하지 않습니다.
- 가스 입자는 일정한 무작위 운동입니다.
- 가스 입자 간의 충돌 또는 입자와 용기 벽 사이의 충돌은 탄력적입니다. 다시 말해, 분자는 서로 고수하지 않고 충돌에서 에너지가 사라지지 않습니다.
이러한 가정에 근거하여 가스는 예측 가능한 방식으로 행동합니다.
- 가스 입자는 무작위로 움직이지만 항상 직선으로 이동합니다.
- 가스 입자가 컨테이너가 움직이고 부딪 치기 때문에 용기의 부피는 가스의 부피와 동일합니다.
- 가스의 압력은 용기 벽과 충돌하는 입자 수에 비례합니다.
- 입자는 온도가 증가함에 따라 운동 에너지를 얻습니다. 운동 에너지 증가는 충돌의 수와 가스 압력을 증가시킵니다. 따라서 압력은 절대 온도에 직접 비례합니다.
- 입자는 모두 동일한 에너지 (속도)를 갖지는 않지만, 그 중 많은 것이 있기 때문에 가스 온도에 비례하는 평균 운동 에너지가 있습니다.
- 개별 입자 사이의 거리는 다양하지만 평균 자유 경로라고 불리는 평균 거리가 있습니다.
- 가스의 화학적 동일성은 중요하지 않습니다. 따라서 산소 가스 용기는 공기 용기와 정확히 동일하게 동작합니다.
이상적인 가스 법은 가스의 특성 사이의 관계를 요약합니다.
pv =nrt
여기서, p는 압력, v는 부피, n은 가스의 두부 수이고, R은 이상적인 가스 상수이며, t는 절대 온도입니다.
.가스의 운동 이론과 관련된 가스 법률
가스의 동역학 이론은 다른 거시적 특성 사이의 관계를 확립합니다. 이상적인 가스 법칙의 이러한 특별한 경우는 특정 값을 일정하게 유지할 때 발생합니다.
- p α n :일정한 온도 및 부피에서 압력은 가스량에 직접 비례합니다. 예를 들어, 용기에있는 가스의 두더지 수를 두 배로 늘리면 압력이 두 배가됩니다.
- v α n (Avogadro 's Law) :일정한 온도 및 압력에서, 부피는 가스량에 직접 비례합니다. 예를 들어, 가스 입자의 절반을 제거하면 압력이 동일하게 유지되는 유일한 방법은 부피가 절반으로 감소하는 것입니다.
- p α 1/v (Boyle 's Law) :가스의 양과 온도가 변경되지 않은 것으로 가정하여 부피가 감소함에 따라 압력이 증가합니다. 다시 말해, 가스는 압축 가능합니다. 온도를 바꾸지 않고 압력을 가할 때 분자는 더 빨리 움직이지 않습니다. 부피가 감소함에 따라 입자는 용기 벽까지 짧은 거리를 이동하여 더 자주 공격합니다 (압력 증가). 부피가 증가하면 입자가 컨테이너 벽에 도달하고 자주 덜 공격하기 위해 더 많은 입자가 이동한다는 것을 의미합니다 (압력 감소)
- v α t (Charles 'Law) :가스 부피는 일정한 압력과 가스의 양을 가정 할 때 절대 온도에 직접 비례합니다. 다시 말해, 온도를 높이면 가스가 양이 증가합니다. 온도를 낮추면 양이 줄어 듭니다. 예를 들어, 이중 가스 온도는 양을 두 배로 늘립니다.
- p α t (게이 -lussac 또는 Amonton 's Law) :질량과 부피를 일정하게 유지하면 압력은 온도에 직접 비례합니다. 예를 들어, 삼중 온도는 압력을 3 배로 늘립니다. 가스의 압력을 방출하면 온도가 낮아집니다.
- v α (1/m) (Graham 's Fiffusion의 법칙) :가스 입자의 평균 속도는 분자량에 직접 비례합니다. 또는 두 개의 가스 비교, v 1 /v 2 =m 2 /m 1 .
- 운동 에너지 및 속도 :평균 운동 에너지 (KE)는 가스 분자의 평균 속도 (뿌리 평균 제곱 또는 RMS 또는 U)와 관련이 있습니다. KE =1/2 MU
- 온도, 어금니 질량 및 rms :운동 에너지와 이상적인 가스 법칙에 대한 방정식을 결합하면 뿌리 평균 제곱 속도 (u)와 절대 온도 및 어금니 질량과 관련이 있습니다. u =(3rt/m)
- Dalton의 부분 압력 법칙 :가스 혼합물의 총 압력은 성분 가스의 부분 압력의 합과 같습니다.
예제 문제
계산 rms 속도
분자가 3.0, 4.5, 8.3 및 5.2 m/s의 속도를 갖는 경우 가스에서 분자의 평균 속도와 RMS 속도를 찾으십시오.
값의 평균 또는 평균은 단순히 합계가 얼마나 많은 값으로 나뉘어져 있습니다 :
(3.0 + 4.5 + 8.3 + 5.2)/4 =5.25 m/s
그러나 루트 평균 제곱 속도 또는 RMS는 속도 제곱 합의 제곱근을 총 값 수로 나눈 값입니다.
u =[(3.0 + 4.5 + 8.3 + 5.2)/4] =5.59 m/s
온도에서 rms 속도
298k에서 산소 가스 샘플의 RMS 속도를 계산합니다.
온도는 켈빈 (절대 온도)에 있기 때문에 단위 변환이 필요하지 않습니다. 그러나 산소 가스의 몰 질량이 필요합니다. 산소의 원자 질량에서 이것을 얻으십시오. 분자 당 2 개의 산소 원자가 있으므로 2를 곱한 다음 두더지 당 그램에서 두더지 당 킬로그램으로 변환하여 단위가 이상적인 가스 상수의 유닛과 메쉬로 변환합니다.
.mm =2 x 18.0 g/mol =32 g/mol =0.032 kg/mol
u =(3rt/m) =[(3) (8.3145 j/k · mol) (298 k)/(0.032 kg/mol)]
Joule은 Kg⋅m⋅s입니다.
u =482 m/s
참조
- 시드니 채프먼; Cowling, Thomas George (1970). 불균일 가스의 수학적 이론 :가스의 점도, 열 전도 및 확산의 동역학 이론 (제 3 판). 런던 :Cambridge University Press.
- Grad, Harold (1949). "희귀 가스의 동역학 이론에." 순수하고 응용 수학에 대한 커뮤니케이션 . 2 (4) :331–407. doi :10.1002/cpa.3160020403
- Hirschfelder, J. O.; 커티스, C.F.; Bird, R. B. (1964). 가스 및 액체의 분자 이론 (Rev. ed.). Wiley-Interscience. ISBN 978-0471400653.
- Maxwell, J. C. (1867). “가스의 역학 이론에”. 런던 왕립 학회의 철학적 거래 . 157 :49–88. doi :10.1098/rstl.1867.0004
- Williams, M. M. R. (1971). 입자 수송 이론의 수학적 방법 . 버터 워스, 런던. ISBN 9780408700696.