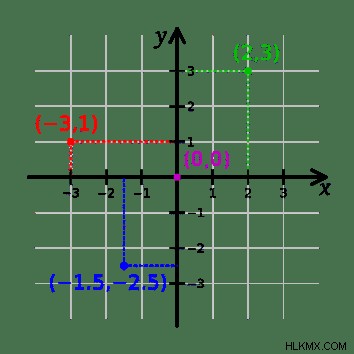
사분면 2 차원 데카르트 시스템이 분할되는 방법과 포인트 그래프 의 가치 그 안에서 X 축 및 Y 축에 대한 위치에 따라 다릅니다. 사분면은 평면을 4 개의 별도 영역으로 나누고, 각 영역은 축의 절반으로 제한됩니다.
그들은 일반적으로 로마 숫자를 식별하기 위해 로마 숫자가 주어지고, 오른쪽 상단에서 오른쪽 바닥으로 시계 반대 방향으로 움직입니다. i, ii, iii 및 iv.
.직교 그래프/평면의 사분면 정의
사분면은 평면을 두 축으로 나눈 값을 기준으로합니다. x 축은 수평 축이고 y 축은 수직 축입니다. 두 축의 교차점은 x와 y 값이 모두 0 인 곳입니다. 양의 Y 값은 수평선 위에서 발견되는 반면 음수 값은 그 아래에 있습니다. 마찬가지로, 양의 x 값은 y 축의 오른쪽에 발견되고 y 축의 왼쪽에있는 음의 x 값이 발견됩니다.
따라서, 사분면 I은 두 값이 양수 ( +, +)이고 사분면 II는 x가 음수이지만 y는 양수 (-, +) 인 값을 함유하는 지점을 포함합니다. 사분면 III은 두 값 모두 음수 ( -, -) 인 지점을 포함하고 사분면 IV에는 x가 양수이지만 y는 음수 (+, -).
삼각법에는 직교 비행기에 플로팅 할 수있는 세 가지 기능이 있습니다. 그들은 사인, 코사인 및 탄젠트입니다. 사인 그래프는 0에서 시작하여 π/2 라디안 (90 °)으로 최대 1으로 이동 한 다음 -1로 이동하는 그래프입니다. 대칭적인 위쪽 곡선이 있습니다. 코사인은 0이 아닌 1에서 시작하고 -1로 다시 아래쪽으로 이동할 때까지 π 라디안 (180 °)에 의해 상승하는 플롯입니다. 원점을 제외하고는 사인의 음모와 비슷해 보입니다. 한편, 탄젠트 기능은 다른 두 기능과는 다른 모양을 갖습니다. 탄젠트 기능은 음성과 양의 무한대 사이에서 실행되지만 0의 원점을 통과하며 모든 π 라디안 (180 °)에서 교차합니다. 이것은 얕은 곡선을 반복하는 패턴을 제공합니다.
사분면 I에서는 사인, 코사인 및 탄젠트의 모든 플롯이 양수가 될 것입니다. Quadrant II에서는 sine, cosec (sine) 그래프 만 긍정적입니다. 사분면 III에서는 황갈색과 침대 (탄젠트) 플롯 만 양수가 될 것이며, 사분면 IV에서는 COS and SEC (COSINE) 플롯이 양수가 될 것입니다. 이것에 대한 니모닉은“모든 과학 교사들 (미친)입니다.
데카르트 비행기/좌표 시스템은 프랑스 철학자이자 수학자 인 르네 데카르트 (Rene Descartes)로부터 이름을 얻었습니다. 그는 1637 년에 아이디어를 생각해 내고 그 아이디어를 발표했습니다. 피에르 드 페르 매트 (Pierre de Fermat)가 독립적으로 만들었습니다. 데카르트와 Fermat은 모두 좌표계 버전에서 단일 축을 사용했지만 나중에 수학자들은 작업을 확장하고 두 축으로 시스템을 표준화 할 것입니다.
.변환

유클리드 변형 또는 유클리드 모션은 유클리드 평면 내에서 지점의 거리를 보존하는 다른 지점으로의 이동/매핑입니다. 회전, 번역, 반사 및 활공 반사의 네 가지 유형의 변환이 있습니다.
유클리드 회전은 중심에서 어느 지점까지 어느 지점까지의 거리가 동일하게 유지되고, 점수가 선택된 모양의 중심 주위에서 회전 함을 의미합니다. 반사는 평면의 축 중 하나에 모양이나 기하학적 물체가 뒤집 혔음을 의미합니다. 이것은 선택된 지점이 축을 다른 사분면으로 가로지게한다는 것을 의미합니다. 예를 들어, 포인트가 4, -3으로 표시되면,이 점의 반사는 -4, 3으로 만들어집니다. 글라이드 반사는 모양이 먼저 반사 된 다음 번역 된 후 번역 된 특정 유형의 반사입니다. 기하학적 형상의 번역은 모양이 주어진 크기의 변화로 주어진 방향으로 움직임을 의미합니다. 번역의 핵심 요점은 모양의 모든 지점이 같은 거리로 동일한 방향으로 움직여야한다는 것입니다.
2 차원의 데카르트 시스템
x 축을 선택하면 y 축 방향이 결정됩니다. y 축은 x 축에 수직이며 x 축에서 0으로 표시된 지점을 통과합니다. 그러나 라인의 두 반쪽의 절반이 양수 또는 부정적으로 표시되는 선택을 선택할 수 있습니다. 이 선택은 직교 비행기에 방향이나 손을주는 것입니다. 즉, 어떤 방향이 양의 또는 음수인지를 선택하는 것이 그래프의 제작자에게 달려 있지만, 양수/네거티브 영역에 라벨을 붙이는 정상적인 방법은 양의 x 축을 오른쪽으로 달리는 동안 양의 y 축이 실행되는 것입니다.
.벡터에 대한 메모
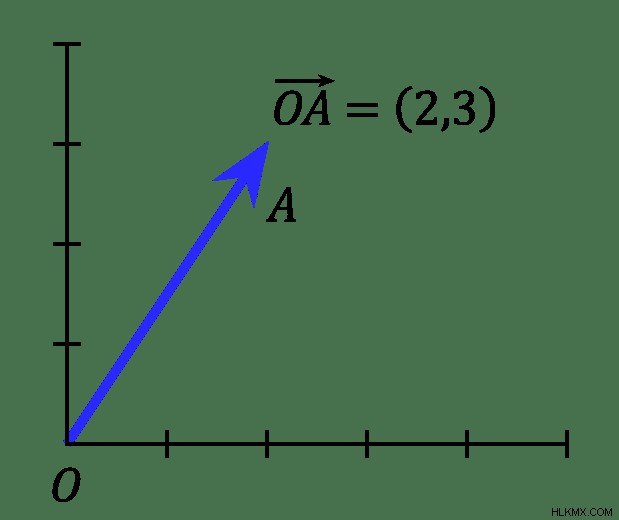
데카르트 좌표계의 점은 또한 좌표 평면 (0, 0)의 기원에서 지점까지의 벡터 또는 화살표로 정의 될 수 있습니다. 벡터에는 방향과 크기의 두 가지 특성이 있습니다. 방향은 벡터가 움직이는 방향 (위, 아래, 왼쪽, 오른쪽)입니다. 크기는 그 방향의 움직임량을 나타냅니다. 좌표가 공간 위치에 대한 스탠드 인 경우, 원점에서 시작하여 지점으로 이동하는 벡터는 일반적으로 "r"으로 표시됩니다. 원점에서 지점까지 존재하는 벡터는 일반적으로 r =xi, + yj로 표시됩니다. "I"및 "J"는 각각 (1/0)과 (0/1)이며 X 및 Y 축의 관점에서 벡터의 방향을 나타냅니다.
직교 비행기의 그래프
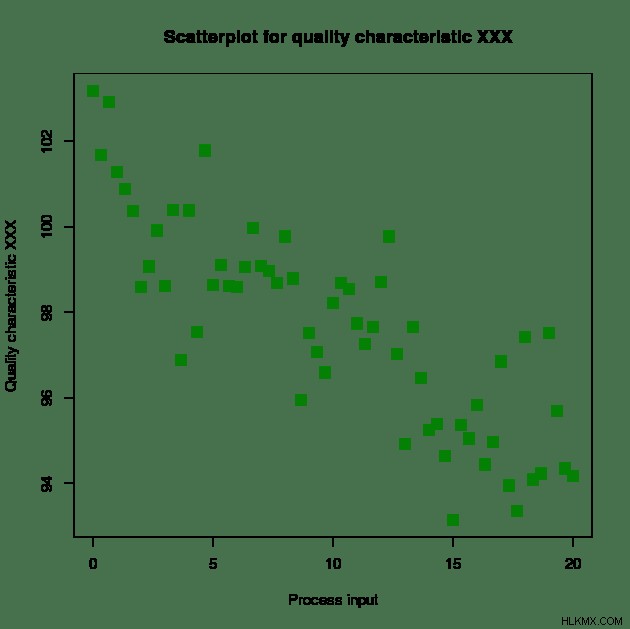
직교 그래프는 직교 비행기에 표시 할 수있는 그래프입니다. 그들은 서로 선형 관계로 표현 될 수있는 데카르트 그래프에 포인트를 보여줍니다.
라인 플롯은 직교 비행기에서 생성 된 가장 기본적인 유형의 플롯/그래프입니다. 시간이 지남에 따라 수량이 어떻게 변하는 지와 같이 두 변수가 서로 관련되는 방식을 시각화하는 데 사용됩니다. 라인 플롯에는 하나의 변수가 다른 변수와 관련하여 어떻게 변하는 지에 대한 관련 정보를 제공하는 일련의 포인트가 있습니다. 라인 세그먼트는 포인트를 연결하고 트렌드를 표시하는 데 사용됩니다.
또 다른 일반적인 유형의 그래프는 산점도로, 주어진 데이터 세트에 대해 두 가지 변수의 개별 인스턴스/발생을 보여줍니다. 관계가 존재하는 경우 두 가지 정량적 변수 간의 관계를 결정하는 데 사용됩니다.







