평형은 신체에 작용하는 모든 힘이 0과 같은 역학에서 특별한 경우입니다. 이러한 유형의 문제는 많은 상황에서 팝업되며 엔지니어링 및 물리학에서 중요합니다. 이 평형 예제 문제는 평형 상태에서 신체에 작용하는 힘의 시스템에 작용하는 다른 힘을 결정하는 방법을 보여줍니다.
예제 문제 :
무게 w 블록은 지점 O의 다른 두 개의 로프에 묶인 로프에서 매달려 있습니다. 한 밧줄은 벽에 수평으로 부착되고 다른 로프는 천장에 고정됩니다. 천장과 로프 사이의 각도는 60 °입니다. 각 로프의 긴장은 무엇입니까? 로프의 무게와 매듭이 무시할 수 있다고 가정하십시오. 블록의 무게가 100 N이면 천장 로프의 장력은 얼마입니까?
솔루션 :
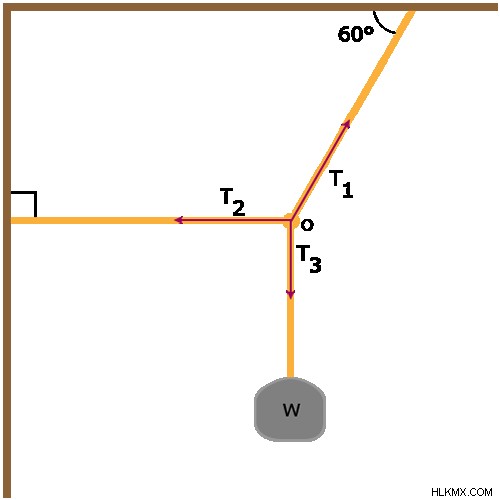
이 그림은 문제에 설명 된 배열을 보여줍니다.
모든 장력력은 O 지점에서 매듭에 작용합니다. 변수는 다음과 같이 정의되었습니다.
t 1 =천장 로프의 장력
t 2 =벽 밧줄의 장력
t 3 =블록 로프의 장력
고려해야 할 다른 시스템이 있습니다. t 3 사이의 연결 로프와 블록. 이 시스템은 블록의 무게를 로프의 장력과 관련시키기 때문에 유용합니다. 이것은 차례로 블록의 무게를 다른 두 개의 로프의 긴장과 관련시킵니다.
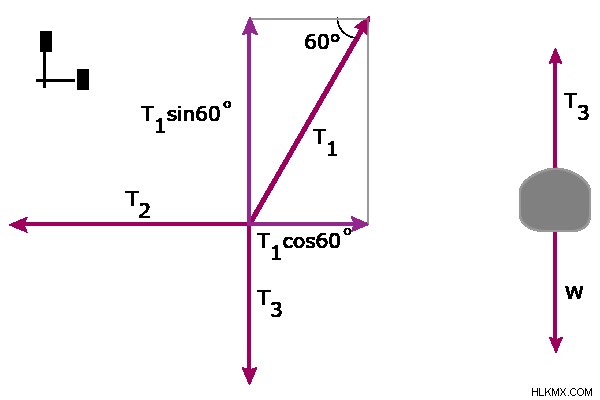
두 시스템의 첫 번째 힘 도표를 그려냅니다.
좌표계는 x 축을 따라 수평으로 표시되고 y 축을 따를 수있는 수직을 보여줍니다. t 3 에 주목하십시오 그리고 W는 블록에서 작용하는 유일한 두 힘이다. 이것은 실제로 블록에 연결된 유일한 두 힘이기 때문입니다. 이 시스템부터 시작하겠습니다. 좌표계별로 힘을 그룹화하십시오.
X 방향에서 :블록에 작용하는 힘이 없습니다
σf x =0
y 방향의 경우, t 3 무게 W가 부정적인 방향으로 블록을 아래로 당기는 동안 블록을 양수 방향으로 끌어 올리고 있습니다. 블록은 고정식 (평형) 이므로이 두 힘의 총계는 0입니다.
σf y =0
σf y =t 3 + (-W)
또는
σf y =t 3 - w
이 두 방정식은 모두 같은 것과 같기 때문에 서로 동일해야합니다.
0 =t 3 - w
또는
t 3 =W
이제 우리는 첫 번째 로프에 긴장이 있습니다. 이제 다른 두 개의 로프에서 긴장을 찾아 보겠습니다. 그림에서 천장 밧줄의 힘이 수평 및 수직 구성 요소로 어떻게 나뉘어 지는지에 유의하십시오. 이것은 좌표계를 따라 모든 힘을 더 쉽게 추가 할 수있게 해줄 것입니다.
먼저, 세로 축을 따라 힘을보십시오. t 1 의 수직 성분 t 3 동안 양의 y 방향으로 매듭을 당기고 있습니다. 음의 y 방향으로 매듭을 아래로 당기고 있습니다. t 1 의 수직 성분 t 1 입니다 sin60 °.
σf y =t 1 sin60 ° + (-t 3 ))
σf y =t 1 sin60 ° - t 3
다시, 매듭은 고정되어 있고 평형 상태이므로 힘의 합은 0과 같습니다.
0 =t 1 sin60 ° - t 3
t 3 =t 1 sin60 °
우리는 t 3 을 알고 있습니다 이전의 W와 같습니다. 이 방정식은 다음과 같습니다.
w =t 1 sin60 °
sin60 ° =0.866 :
사용w =(0.866) t 1
t 1 에 대해 해결하십시오 :
t 1 =(1.155) w
두 개의 긴장과 하나는 갈 것입니다. 최종 장력의 경우 수평 축을 따라 작용하는 힘을보십시오. t 1 수평 구성 요소는 양의 X 방향으로 매듭을 당기고 T 2 음의 X 방향을 당기고 있습니다. t 1 의 수평 성분 t 1 입니다 cos60 °.
σf x =t 1 cos60 ° + (-t 2 ))
σf x =t 1 cos60 ° - t 2
매듭은 고정되어 있기 때문에 매듭은 평형 상태이고 σf x =0.
0 =t 1 cos60 ° - t 2
또는
t 2 =t 1 cos60 °
우리는 그 위에서 그 t 1 를 알고 있습니다 =(1.155) w. 이것을 t 1 의 방정식에 연결하십시오 .
t 2 =(1.155) w · cos60 °
계산기에서 우리는 COS60 ° =0.5
를 알고 있습니다
t 2 =(1.155) w · (0.5)
t 2 =0.577W
이제 우리는 로프의 모든 긴장을 알고 있습니다.
t 1 =w
t 2 =0.577W
t 3 =1.155W
문제의 두 번째 부분은 w의 값을 100 N과 동일하게했습니다.이 값을 긴장으로 대체합니다.
t 1 =115.5 n
t 2 =57.7 n
t 3 =100 n
이 문제는 특히 천장 로프의 긴장을 요구했습니다. 천장 로프는 t 1 였습니다 로프 및 t 1 =115.5 n.
이러한 유형의 문제의 핵심은 시스템을 분리하고 개별 부품에서 작용하는 모든 힘을 찾는 것입니다. 시스템이 평형 상태이기 때문에이 모든 힘의 합은 0과 같습니다.