발사체를 던지거나 촬영하는 것은 포물선 코스를 따릅니다. 발사체의 초기 속도와 상승 각도를 알고 있다면 시간 내내 최대 높이 또는 범위를 찾을 수 있습니다. 시간이 주어지면 고도와 거리가 이동할 수도 있습니다. 이 예제 문제는이 모든 작업을 수행하는 방법을 보여줍니다.
발사체 모션 예제 문제 :
대포는 고도 각도 =45 °에서 150m/s의 총구 속도로 발사됩니다. 중력 =9.8 m/s.
a) 발사체가 도달하는 최대 높이는 얼마입니까?
b) 총 시간은 얼마입니까?
c) 발사체 땅은 얼마나 멀리 떨어져 있었습니까? (범위)
d) 발사 후 10 초에 발사체는 어디에 있습니까?
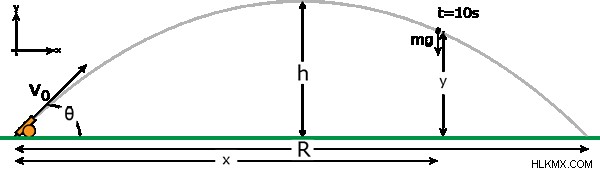
우리가 알고있는 것을 설정합시다. 먼저 변수를 정의해 봅시다.
v 0 =초기 속도 =총구 속도 =150 m/s
v x =수평 속도 구성 요소
v y =수직 속도 구성 요소
θ =고도 각도 =45 °
h =최대 높이
r =범위
x =t =10 s에서 수평 위치
y =t =10 s에서 수직 위치
m =발사체 질량
g =중력으로 인한 가속도 =9.8 m/s
파트 a) 찾기 h.
우리가 사용할 공식은 다음과 같습니다.
d =v 0 t + ½at
그리고
v f - v 0 =at
거리 H를 찾으려면 H의 속도와 거기에 도착하는 데 걸리는 시간의 두 가지를 알아야합니다. 첫 번째는 쉽습니다. 속도의 수직 성분은 지점에서 0과 같습니다. 이것이 상향 운동이 멈추고 발사체가 지구로 떨어지기 시작하는 지점입니다.
초기 수직 속도는입니다
v 0y =v 0 · sinθ
v 0y =150 m/s · sin (45 °)
v 0y =106.1 m/s
이제 우리는 시작과 최종 속도를 알고 있습니다. 다음으로 필요한 것은 가속입니다.
발사체에 작용하는 유일한 힘은 중력의 힘입니다. 중력은 g의 크기와 음의 y 방향으로 방향을 갖습니다.
f =ma =-mg
를 해결하십시오
a =-g
이제 우리는 시간을 찾기에 충분한 정보가 있습니다. 우리는 초기 수직 속도 (v 0y 를 알고 있습니다 ) 및 H에서의 최종 수직 속도 (v hy =0)
v hy - v 0y =at
0 - v 0y =-9.8 m/s · t
0 -106.1 m/s =-9.8 m/s · t
t
에 대한 해결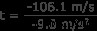
t =10.8 s
이제 h
의 첫 번째 방정식을 해결하십시오
h =v 0y t + ½ at
h =(106.1 m/s) (10.8 s) + ½ (-9.8 m/s) (10.8 s)
H =1145.9 m - 571.5 m
H =574.4 m
발사체에 도달하는 가장 높은 높이는 574.4 미터입니다.
파트 B :총 시간을 찾으십시오.
우리는 이미 당신이 생각을 멈추면 질문 의이 부분을 얻기 위해 대부분의 작업을 수행했습니다. 발사체의 여행은 두 부분으로 나눌 수 있습니다.
t 총 =t up + t down
동일한 가속력이 양방향으로 발사체에 작용합니다. 시간이 다가 오는 데 걸리는 시간과 같은 시간이 걸립니다.
t up =t down
또는
t 총 =2 t up
우리는 t up 를 발견했습니다 문제의 부분에서 :10.8 초
t 총 =2 (10.8 s)
t 총 =21.6 s
발사체의 총 시간은 21.6 초입니다.
파트 C :범위 r 을 찾으십시오
범위를 찾으려면 X 방향의 초기 속도를 알아야합니다.
v 0x =v 0 cosθ
v 0x =150 m/s · cos (45)
v 0x =106.1 m/s
범위 r을 찾으려면 방정식을 사용하십시오.
r =v 0x t + ½at
x 축을 따라 작용하는 힘은 없습니다. 이것은 X 방향의 가속도가 0임을 의미합니다. 운동 방정식은 다음과 같습니다.
r =v 0x t + ½ (0) t
r =v 0x t
범위는 발사체가 문제의 파트 B에서 발견 한 시점에 발생하는 땅을 때리는 지점입니다.
r =106.1 m/s · 21.6s
r =2291.8 m
발사체는 캐논에서 2291.8 미터에 착륙했습니다.
파트 D :t =10 초에 위치를 찾으십시오.
위치에는 수평 및 수직 위치의 두 가지 구성 요소가 있습니다. 수평 위치 인 X는 발사체가 발사 후에 있고 수직 구성 요소는 발사체의 현재 고도 y입니다.
.이 위치를 찾으려면 동일한 방정식을 사용합니다.
d =v 0 t + ½at
먼저, 수평 위치를하겠습니다. 수평 방향에는 가속도가 없으므로 Part C에서와 같이 방정식의 후반부는 0입니다.
x =v 0x t
우리는 t =10 초가 주어집니다. v 0x 문제의 파트에서 계산되었습니다.
x =106.1 m/s · 10 s
x =1061 m
이제 수직 위치에 대해 동일한 작업을 수행합니다.
y =v 0y t + ½at
우리는 파트 B에서 v 0y 를 보았다 =109.6 m/s 및 a =-g =-9.8 m/s. t =10 s :
y =106.1 m/s · 10 s + ½ (-9.8 m/s) (10 초)
y =1061 - 490 m
y =571 m
T =10 초에 발사체는 (1061m, 571m) 또는 1061m 하향 조정 및 고도 571 미터입니다.
특정 시간에 발사체의 속도를 알아야하는 경우 공식을 사용할 수 있습니다.
v - v 0 =at
그리고 v. v. velocity는 벡터이며 x와 y 구성 요소를 모두 가지고있을 것입니다.
이 구체적인 예는 초기 속도와 상승 각도에 쉽게 적응할 수 있습니다. 대포가 다른 중력의 힘으로 다른 행성에서 발사되면 그에 따라 g의 값을 바꾸십시오.







