특수 상대성 이론은 시간에 대한 흥미로운 개념을 소개했습니다. 기준 프레임을 움직일 때 시간은 동일한 속도로 전달되지 않습니다. 움직이는 시계는 고정식 참조 프레임에서 시계보다 느리게 작동합니다. 이 효과는 시간 확장이라고합니다. 이시기 차이를 계산하기 위해 Lorentz 변환이 사용됩니다.
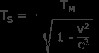
어디
t m 움직이는 기준 프레임에서 측정 된 시간 지속 시간입니다.
t s 고정 기준 프레임에서 측정 된 시간 지속 시간입니다.
v는 움직이는 기준 프레임의 속도입니다.
C는 빛의 속도
시간 팽창 예제 문제
이 효과가 실험적으로 입증 된 한 가지 방법은 고 에너지 뮤온의 수명을 측정하는 것이 었습니다. Muons (기호 μ)는 전자 및 2 개의 중성미자로 붕괴되기 전에 평균 2.2 μsec에 대해 존재하는 불안정한 기본 입자입니다. 우주 광선 방사선이 대기와 상호 작용할 때 뮤온은 자연적으로 형성됩니다. 그것들은 존재의 시간이 정확하게 측정 될 수있는 입자 콜라이더 실험의 부산물로 생성 될 수 있습니다.
뮤온은 실험실에서 생성되어 8.8 μsec에 존재하는 것으로 관찰됩니다. 뮤온이 얼마나 빨리 움직였습니까?
솔루션
Muon의 기준 프레임에서 2.2 μsec의 경우 존재합니다. 이것은 t m 입니다 우리 방정식의 가치.
t s 8.8 μsec에서 정적 기준 프레임 (실험실)에서 측정 된 시간 또는 존재하는 것보다 4 배입니다. t s =4 t m .
우리는 속도를 위해 해결하고 싶습니다. 방정식을 조금 단순화합시다. 먼저, 양쪽을 t m 로 나눕니다 .
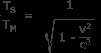
방정식을 뒤집어
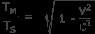
라디칼을 제거하기 위해 양쪽을 제곱합니다.
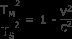
이 양식은 작업하기가 더 쉽습니다. t s 를 사용하십시오 =4 t m 얻는 관계
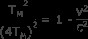
또는
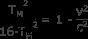
t m 를 취소하십시오 떠나기 위해
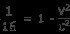
양쪽에서 1을 빼십시오
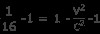
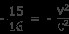
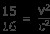
양쪽에 c
를 곱하십시오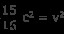
양쪽의 제곱근을 가져 가서 v
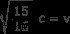
v =0.968c
답변 :
뮤온은 빛의 속도 96.8%로 움직이고있었습니다.
이러한 유형의 문제에 대한 중요한 참고 사항 중 하나는 속도가 측정 가능하고 눈에 띄는 차이를 만들기 위해 속도의 몇 배 안에 있어야한다는 것입니다.
.