고전적인 공상 과학 소설의 모험 Flatland Edwin Abbott에 의해 생겨났다. 이 소설은 자신을 "광장"이라고 부르는 2 차원 생물에 의해 나레이션되며, 그는 자신을 알지 못하고 Spaceland라는 3 차원 영역에 내장되었다는 것을 알게된다. Square 씨와 마찬가지로 지난 세기 동안의 물리학 자들은 우리 세계가 4 차원 또는 10 차원의 한 조각 일지 여부를 고려하기 시작했습니다. 만약 우리가 그 높은 영역으로 올라갈 수 있다면, 우리는 평범한 공간의 구속력에서 벗어날 것입니다. 우리는 추가 치수를 통해 팔을 구부리기 위해 잠긴 금고에 도달하거나 우리 앞에 놓인 인체의 내부를 볼 수있었습니다. 그리고 우리는 마침내 자연의 깊은 통일성을 이해할 수 있습니다.
그러나 최근 몇 년 동안 치수 사가는 호기심 많은 비틀기를 가져 왔습니다. 공간은 우리 주변에서 인식하는 것보다 더 많은 차원이 없을 수도 있지만 .
차원 수축은 자연의 네 가지 기본 힘 중 하나 인 중력 문제를 해결합니다. 몸이 가까워지면서 두 몸 사이의 중력 매력이 강해집니다. 그것은 또한 전자기 및 약한 힘과 같은 다른 힘에게도 마찬가지입니다. 그러나 이러한 힘과 달리 중력은 작은 규모로 추가로 강화됩니다. 매력적인 힘은 신체의 질량 또는 동등한 에너지에 달려 있으며, 양자 물리학의 불확실성 원리는 그 에너지의 양이 최소로 이어집니다. 신체가 서로 충분히 가까워지면, 그 최소값은 거리에 대한 역에 비례하여 증가하기 시작하여 붉어진 강도로 끌어 당깁니다. 자연의 다른 힘은 또한 양자 강화 또는 약화를 거치지 만 훨씬 적은 정도입니다. 결과적으로, 일상적인 척도의 푸시 오버 인 중력은 다른 힘을 따라 잡고 플랑크 스케일 (planck scale)으로 알려진 서브 서브 바토 학자 거리 (미터 1 조의 1 조의 약 2 조의 약 1 조의 약 1 조
실제로, 표준 중력 이론은이 척도에서 중력이 너무 강해져 문제가 블랙홀로 무너질 것이라고 예측합니다. 중력은 시공간의 모양을 반영하기 때문에 무한한 강화는 시공간 연속체가 파쇄에 찢어 지므로 우리가 일상 생활에서 경험하는 특징이없는 공간이 현실의 근본적인 특징이 될 수 없음을 시사합니다. 다른 구조는 다른 구조를 대체해야하거나 무언가 중력이 작은 규모로 날아가는 것을 절약하여 시공간의 기본 상태 또는 둘 다를 보존해야합니다. 어느 쪽이든, 표준 이론은 불완전해야합니다.
시공간의 미세한 구조는 양자 중력의 문제로, 아인슈타인의 물리학 자들이 흘렀다. 3 명의 이론가를 방에 넣으면 그것이 무엇인지에 대한 4 가지 아이디어를들을 수 있습니다 :체스 보드와 같은 개별 셀 아레나, 변동하는 지오메트리의 폼, 진동 줄의 응축수, 짜여진 루프의 직물 등.
.놀랍게도, 이론가들은 이제 이러한 다양한 가능성이 공통적 인 특징을 가지고 있음을 발견하고 있습니다. 가장 훌륭한 규모의 공간은 모든 차원을 흘리며 하나는 과정에서 중력을 길들이는 중력을 훼손합니다. 사실, 1 차원 공간은 거리가 줄어들면서 중력의 힘이 폭발하지 않는 유일한 장소입니다.
치수 수축이 시공간을 자연의 근본적인 특징으로 절약하는지 여부는 최종 실종의 전주인지는 불분명합니다. 그러나 네덜란드의 Radboud University의 이론적 물리학자인 Frank Saueressig의 말에 따르면“두 차원 [한 공간과 한 번]은 중력이 살고 싶어하는 자연적인 차원 인 것 같습니다.
.flatland 의 언어로 , 우리는 모두 우주선이 아니라 Lineland에 살고있을 수 있습니다.
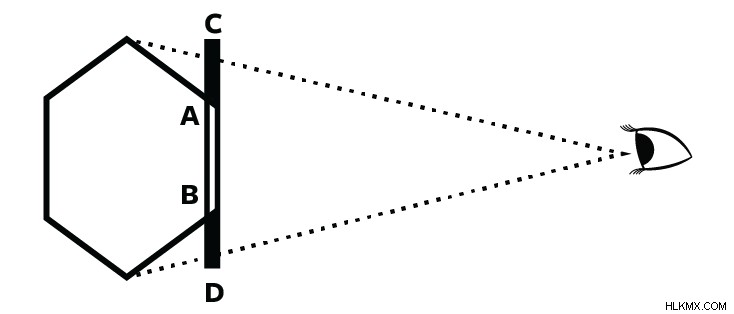
공간의 차원이 보일 수있는 것처럼 신비한 것처럼, 그것은 매우 실질적인 의미를 가지고 있습니다. 그것은 물체의 크기, 사건의 속도 및 상황이 점점 커지면 힘의 강도가 어떻게 변할 때, 힘의 강도가 어떻게 변하는 지 결정합니다. 평범한 3D 공간에서 구의 반경을 두 배로 늘리면 볼륨이 8 배 증가합니다. 4D 공간에서는 16 배 증가 할 것입니다. 2D에서는 4 배만.
따라서 공간이 얼마나 많은지를 알지 못했다면 볼륨의 규모로부터 유추 할 수 있습니다. 그리고 스케일링 관계가 고정되어 있지 않다는 것을 알게되면 구체의 반경을 두 배로 늘리고 부피가 더 이상 8 배 증가하지 않으면 공간의 차원이 다양하다는 것을 분별했습니다.
.그것이 많은 물리학 자들이 의심되는 일입니다.
이 라인을 따라 생각하게 한 것은 2000 년대 중반의 시공간의 플랑크 스케일 모양의 일련의 컴퓨터 시뮬레이션이었습니다. Radboud에있는 Renate Loll과 그녀의 동료들은 인과 적 동적 삼각형이라는 알고리즘을 고안하여 시뮬레이션 된 시공간을 양자 속성으로 촉구했습니다. 그들은 관찰 가능한 척도의 공간이 우리가 경험하는 것처럼 3 차원을 가져야한다는 것을 보여줄 수있었습니다. 그러나 중력의 강도가 다양하다면, 공간이 더 적은 치수를 가진 트리와 같은 구조로 전환 될 수 있거나, 마치 공간이 얼거나 끓는 것처럼 거의 더 많은 구겨진 wad로 전환 될 수 있습니다.
그리고 공간이 3D를 안심할 수 있더라도 그 외관이됩니다. 연구원들은 가스 분자가 볼륨을 둘러싼 동안 가스 분자와 마찬가지로 각 단계를 임의의 방향으로 취하는 구불 구불 한 산책을 상상했다고 상상했습니다. 3D 공간에서 여행 길이를 두 배로 늘리면 출발점으로 돌아올 가능성이 8의 제곱근으로 떨어집니다. 그러나 시뮬레이션은 마치 손실 할 공간이 적은 것처럼 플랑크 스케일 근처에서 느리게 감소하는 것을 발견했습니다. 이는 치수가 적은 징후입니다.
.볼륨 측정에 따르면 공간은 3D이지만 임의의 동작의 동작에 의해 1-D 또는 분수 차원입니다. 이 불일치는 공간이 덜 넓게 나오는 것뿐만 아니라 중력이 양자 측면을 보여주기 시작함에 따라 그 자연이 바뀌 었다는 신호입니다. 데이비스 캘리포니아 대학교 (University of California)의 스티브 칼립 (Steve Carlip)은“정상적인 매니 폴드가 없으면 일반적으로 '치수'에 대한 다양한 정의가 있습니다.
모든 과학 영역의 컴퓨터 시뮬레이션과 마찬가지로 인과 적 동적 삼각 측량은 블랙 박스입니다. 입력으로 방정식을 취하고 출력으로 숫자를 생성하지만 무슨 일이 일어나고 있는지, 그 이유를 알려주지 않습니다. Loll은“여전히 미스터리입니다. 실제로 무엇을 의미 하는가. 지금까지, 이러한 차원 체조를 설명하는 데 가장 가까운 이론은 1970 년대 후반에 거슬러 올라가는 양자 중력의 어두운 horse 후보 인 점근 적 안전이라고합니다. Gravity에는 일종의 내장 주지사가 있다고 가정하여“안전하다”고 생각합니다. 우리가 일상 생활에서 보지 못하는 중력의 특징은 플랑크 규모 근처에서 일상 생활을 시작하므로, 힘은 제한없이 강화하는 대신 유한 최대 강도에 도달합니다. 점근 적 안전은 많은 입자 물리학 자에게 호소력이 있기 때문에 중력은 원자 핵을 지배하는 힘과 같다는 것을 의미합니다.
점근 적 안전에 따르면, 공간은 분쇄 된 소다 캔처럼 평평 해지 기 때문에 치수를 잃어 버리지만, 양자 효과로 인해 열광적으로 변동하여 입자가 세상을 탐색하는 일반적인 규칙을 변경하기 때문입니다. 예를 들어, 무작위로 캐롤링 입자는 경로에 대한 기억을 유지하고 70 년대의 비디오 게임 뱀과 같이 이미 있었던 곳을 피할 수 있습니다. Saueressig는 그 움직임에 대한 이러한 제약으로 인해 입자는 출발점으로 돌아올 확률이 높아서 더 적은 차원을 통해 움직일 수있는 영향을 줄 수 있다고 말합니다.
.차원 또는 두 가지를 충분히 급진적이지 않은 것처럼 점근 적 안전은 더욱 심오한 공간 변형을 수반합니다. 작은 규모의 중력 고원은 플랑크 스케일 블랙홀을 일으키기에 충분히 강해지지 않으면 표준 이론에서 예측 한 바와 같이 시공간 연속체는 파쇄되지 않습니다. 대신, 그것은 진정으로 연속적인 상태로 남아 있습니다. 제한없이 확대 할 수 있습니다. 그러나 축소하면 신속하게 자신이 혼란 스러울 것입니다. 중력 (그리고 아마도 자연의 다른 힘도)가 더 이상 힘이 증가하지 않으면 한 척도가 다른 규모를 구별하는 것은 없습니다. 모든 것이 똑같아 보입니다. 각 부분은 전체와 비슷합니다. 이것은 프랙탈 구조의 정의입니다.
독일 마인츠 대학교에있는 점근 적 안전의 도이 인 마틴 리터 (Martin Reuter)는이 수준의 우주를 난류 유체 :에디 내 에디 내의 에디와 비교합니다. 두 지점 사이의 경로의 길이는 줌 레벨에 따라 달라지기 때문에 거리가 고정 된 의미를 갖는 것을 중단합니다. 영국 해안선이 흔들림을 더 많이 추가 할 때 줌 수준에 따라 달라집니다.
1 차원 공간은 확실히 그 자체로부터 중력을 절약하는 것 같습니다. 그러나 그 장점은 그 자체로 물리학 자들이 공간이 실제로 작은 규모로 차원을 흘리게한다는 것을 설득하기에 충분하지 않습니다. 모든 이론의 첫 번째 테스트는 내부 일관성입니다. 점근 적 안전의 지지자들과 치수의 상실을 암시하는 다른 접근법은 아직 이것을 보여주지 않았다는 것을 공개적으로 인정한다.
사실, 일부 비평가들은 점근 적 안전은 할 수 없다고 생각합니다 블랙홀의 물리학에 빠지기 때문에 일하십시오. 이 우주 싱크 홀의 내부 복잡성은 외부 표면적으로 확장됩니다. 그러나 점근 적 안전을 포함하여 연속체에 공식화 된 모든 이론에서는 복잡성이 내부 부피로 확장되어야합니다. 지지자들은 공간 치수의 수가 있으면 이러한 스케일링 규칙이 변경 될 것이라고 반박합니다.
점근 적 중력이 궁극적 인 이론이 아니더라도, 그것은 공간이 근본적인 공간 수준에서 나오는 추정 이론에 유용한 디딤돌 일 수 있습니다. 독일 포츠담의 Max Planck Physics Institute for Gravitational Physics의 Daniele Oriti는“시공간 없음’과 '일반적인 시공간'사이에‘이상한 시공간이있을 수 있습니다.
실험실 실험은 곧이 문제를 해결하지 못할 가능성이 높습니다. 실제로 현대적인 악기가 조사 할 수있는 것보다 훨씬 작기 때문에 양자 중력과 관련하여 많은 것들이 있습니다. 우주론 관찰이 더 나은 내기입니다. Reuter는 초기 우주가 규모 별 비균형으로 보였다고 지적했다. 모든 크기의 밀도 변화는 같은 크기를 가졌다. 이것은 점근 안전 이론과 자연의 근본적인 특징 인 시공간을 지원합니다. 그러나 다른 이론들은 규모 별 분량에 대한 대안적인 설명을 제공합니다.
차원의 실종을 제안하는 모든 이론이 잘못 되었음에도 불구하고, 으면서 양자 중력의 깊은 특징을 습득 할 수 있습니다. Carlip은“이것이 매우 흥미로운 이유 중 일부입니다. “이것은 매우 다른 접근법이 공통적으로 가지고있는 양자 중력에 대해 깊은 것을 드러낼 수 있습니다. 그러나 우리는 그것이 무엇인지 모릅니다.”
1884 년 Flatland 의 서문에서 , Abbott는 그의 캐릭터의 목소리에서 사각형의 목소리에서 우리가“각각의 차원의 편견의 노예와 비슷한 방법”을 무너 뜨립니다. 오늘날 물리학 자들은 자신의 차원 편견을 버리는 법을 배우고 있습니다. 결국, Square 씨가 쓴 것처럼“자연의 한 번의 터치는 모든 세상을 비슷하게 만듭니다.”
George Musser는 물리 및 우주론의 작가이며 의 저자입니다. 문자열 이론 및 에 대한 완전한 바보 안내서 거리에서 으스스한 행동 (Farrar, Straus 및 Giroux에서 다가오는). 그는 의 선임 편집자였습니다 Scientific American 14 년 동안 American Institute of Physics Science Writing Award를 수상했습니다.