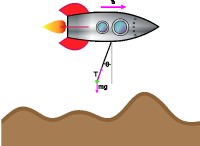
뉴턴의 두 번째 운동 법칙은 물체의 질량, 가속도 및 그에 작용하는 순 힘 사이의 관계를 명시하고 있습니다. 그러나이 법은 움직일 때 체중을 얻거나 잃는 일부 물체에 적용될 수 없습니다. 뉴턴의 운동 법칙과 운동량 계수의 추가로 그러한 물체에 대해 다른 방정식을 도출해야합니다.
가변 질량 시스템 의미
질량이 시간에 따라 다르고 수집 형태 인 문제를 가변 질량 시스템이라고합니다.
파생
계산을 간단하게하기 위해 모든 신체는 입자로 간주됩니다. 가변 질량 시스템의 모션 방정식은 다른 도출을 갖습니다. 방정식은 질량이 떠나거나 들어가는 지에 따라 다릅니다. 가변 질량 시스템의 방정식의 도출은 신체에 의한 질량의 배출 또는 신체에 의한 질량의 부착에 달려있다.
.질량 절제 또는 방출
본체로부터의 질량이 배출되는 시스템에 대한 도출은 절제 될 때와 다릅니다. 대량 m이 시간 t에서 속도 v로 이동하여 시스템의 초기 모멘텀으로 이어집니다.
p 1 =MV
시간 t+ dt에서 질량 DM (절제)의 속도를 봅시다. 그런 다음 시스템에 대한 운동량은
입니다p 2 =(m - dm) (v + dv) - udm =mv + mdv - vdm - dmdv - udm
위의 방정식에서 U는 방출 된 질량의 속도로 간주됩니다. 그것은 질량과 반대되는 방향으로 부정적인 것으로 간주됩니다. DT의 시스템의 운동량은 다음과 같이 제공됩니다.
d p =p 2 - p 1 =(mv+mdv - vdm - dmdv - udm) - (mv) =mdv - (v+dv+u) dm
이제 절제된 질량 m은 상대 속도 v rel 를 가질 것입니다. 다음과 같이
v rel =u- (-V-dv) =v + dv + u
따라서 우리는 운동량으로 변화를 쓸 수 있습니다.
d p =(mv) =mdv v rel DM
따라서 뉴턴의 제 2 법칙에 의해
f ext =d p dt =mdv-v rel dm/dt =m dvdt - v rel dmdt
따라서 최종 방정식은
입니다f ext + v rel dmdt =m dvdt
질량 축적 또는 축적
속도 v에 신체가 움직이고 있습니다. v는 질량 m을 가지고 있으며, 이는 시간과 초기 t에 따라 다릅니다. 동시에, 속도 U가있는 질량 DM을 갖는 입자도 움직이기 시작합니다. 우리는 시작점 (초기 운동량)에서 모멘텀을 쓸 수 있습니다.
p1 =mv+udm
이제 한 번에 t+ dt에서, 본체와 입자가 속도 V+ DV의 몸체로 발생하게하십시오. 우리는 시스템의 새로운 모멘텀을
로 얻습니다p2 =(m+dm) (v+dv) =mv+mdv+vdm+dmdv
DM과 DV의 값은 매우 작으므로 제품을 무시합니다. 시간 DT에서 시스템 운동량은 다음과 같이 변경됩니다.
DP =P2-P1 =(MV+MDV+VDM)-(MV+UDM) =MDV- (U-V) DM
따라서 뉴턴의 제 2 법칙에 의해
f ext =d p DT =MDV- (U-V) DMDT =M DVDT-(U-V) DMDT
우리는 DM이 M과 관련이 있다는 것을 알고 있으며, 이는 속도 u - v를 갖는다. 따라서 U-V를 v rel 로 유지함으로써 , 우리가 얻는 방정식에서
f ext + v rel dmdt =m dvdt
형태
가속도 방정식, a =dv/dt를 사용하여 가변 질량 시스템의 모션 방정식을
로 쓸 수 있습니다.f ext + v rel dmdt =ma
입자 a에 나오지 않으면 몸체를 ACM으로 교체하십시오. 따라서 시스템의 중심 질량은 가속도를 가질 것입니다.
f ext + v rel dmdt =macm
추력으로 인한 힘은 종종 fthrust =vrel dmdtso라고합니다.
fext + fthrust =macm
순 힘이 추력력과 외부 힘의 합으로 취해지면 방정식은 뉴턴의 제 2 법칙으로 돌아갑니다.
fnet =macm
또한, 방정식 Fext + fthrust =macm은 외부 힘이없는 추력으로 인해 신체가 여전히 가속도를 가질 것임을 보여줍니다.
결론
따라서, 가변 질량 시스템에서 운동량이 보존된다는 결론을 내릴 수있다. 가변 질량 시스템에 대한 운동 방정식은 방정식이 질량의 증가 또는 절제 상황에 의존하기 때문에 상이한 도출을 갖는다. 외부 세력이 신체에 작용하지 않더라도 추력력으로 인해 가속화됩니다.