슬래브와 벽을 통한 열 전도의 적용은 최근 기술 개발에 크게 도움이되었습니다. 또한 열 시뮬레이션에서 제제 및 수행을 허용하는 중요한 현상으로 볼 수 있습니다. 몇 가지 요인이 정확도에 영향을 미치지 만 열 흐름을 계산하기위한 방법의 효율성을 이해하는 것이 중요합니다.
슬래브를 통한 열 전도
이제 우리의 주제를 참조하여 슬래브를 통한 열 전도를 이해합시다. 우리가 알다시피, 열 전달 속도는 열 전도도 계수로 정의 된 재료의 특성에 따라 다릅니다. 포함 된 요인은 종종 실험에서 일반적으로 추론되는 간단한 방정식으로 요약됩니다.
그러나 미세한 규모에서, 열전달은 근처 입자와 접촉하는 진동 및 이동 원자와 분자를 통해 빠르게 발생하여 일부 동역학 에너지의 전달이 발생합니다. 열 전도의 적용에 대한 차등 접근법은 수치 솔루션을 나타내는 방법 중 하나입니다. 이들은 슬래브를 통해 열 전도가 발생하는 경우에 더 관련이 있습니다.
열 전도의 전기적 비유
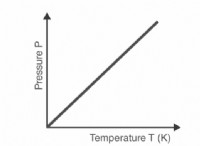
고체의 경우 열 전도는 전기 도체의 경우 전기의 전도와 상당히 동일합니다. 도체의 경우 전위차는 주로 전기 흐름을 주도하는 책임이 있습니다. 열 흐름의 경우 동일한 비유가 적용되며, 온도의 차이에 의해 크게 구동됩니다.
전기 전도에서 전자의 움직임은 전하가 도체의 한 지점에서 다른 지점으로 운반 할 수있게합니다. 더욱이, 열 전도의 경우 분자의 진동과 에너지 증가로 인해 열은 분자의 진동으로 인해 하나의 고체에서 다른 고체로 전달된다. 이 경우 열 전도는 푸리에 법에 의해 규제됩니다.
법은 매체의 두 지점 사이의 열전달 속도 (q)가 분리 (∆x)로 나눈 2 점 (∆x)으로 나뉘어 진 2 점 (T1-T2)의 온도 차이에 비례한다는 것을 암시합니다 (A).
수학적으로 q =ka (t1-t2)/Δx
로 표현됩니다.여기, q =열전달 속도 및 k =재료의 열전도도.
유한 한 층 슬래브를 통한 열 전도
슬래브를 통한 열 전도의 첫 번째 가능한 사례는 한 층 슬래브에 적용 할 수 있습니다. 이 경우 계산을 위해 여러 임의의 상수가 유지됩니다. 여기서는 분석 온도 기능 대신 샘플 값과 해당 타임 인스턴스 만 적용됩니다.
반 유한 1 층 슬래브를 통한 열 전도
방정식 q =ka (t1-t2)/Δx도 반피 나이트 영역의 열 전도 사용 사례에도 적용될 수 있습니다. 그러나 X가 무한대에 적용될 때 솔루션이 제한되도록하는 것이 중요합니다. 결과적으로, 가능한 쌍곡선 기능은 지수 함수로 감소 될 것이다.
이들은 첫 번째 범주의 수정 된 함수와 밀접한 관련이 있지만 세 번째 범주의 수정 된 기능은 지수 함수를 설명하는 데 사용될 수 있습니다.
다층 슬래브를 통한 열 전도
벽 양쪽의 열 흐름 속도와 온도 사이의 관계는 전달 함수로서 작용하는 2 포트 매개 변수로 설명됩니다. 이 매개 변수는 슬래브가 입력 및 출력에만 액세스 할 수있는 영역이되는 데 책임이 있습니다.
그러나 2 포트 매개 변수를 사용하는 것은 특히 다층 벽의 경우 전송 함수를 쉽게 표현하는 방법입니다. 따라서, 다층 슬래브를 통한 열을 올바른 방법을 사용하여 계산하는 것이 중요합니다.
결론
결론적으로, 우리는 슬래브를 통한 열 전도가 일반적으로 알려진 열 전도 방법 중 하나라고 말할 수 있습니다. 이 과정에서, 생성 된 열은 거리를 덮기 때문에 슬래브의 양쪽쪽으로 동일하게 전달되며, 일반적으로 x로 표시됩니다. 이 수량은 X 방향을 따라 슬래브의 중심에서 측정됩니다. 전체 공정 동안, 슬래브 양쪽의 온도는 일정하게 유지되며 T1로 표시되는 반면 동일한 양의 열은 중심에서 슬래브의 다른 측면을 향해 흐릅니다.