3 차원 기하학에서 x, y 및 z 축을 교차하는 선을 라인의 방향 코사인이라고합니다. 그것들은 다음과 같이 정의됩니다. 일관성을 보존하기 위해 문자 L, M 및 N은 종종 이러한 방향성 코사인을 나타내는 데 사용됩니다.
.
코사인 각도는 각 삼각형의 축이 설정된 라인에 의해 형성된 각도 후에 만 결정될 수 있습니다. 라인이 반전 될 때 각도가 변한다는 점에 주목할 가치가 있습니다.
방향 코신 소개
- 원점에 관한 위치를 나타내는 벡터는 위치 벡터라고합니다.
- 방향성 코사인에 대해 이야기하기 전에 위치 벡터를 고려하십시오.
- X, Y, Z라는 3 개의 평면이 3 일 공간에서 O를 사용하여 OQ가 기준선이고 OQ 라인의 길이는 Q입니다. 입니다.
- Q는 가변 Q를 가진 공간의 벡터입니다.
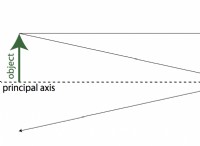
- 지시 된 라인 OQ가 원점을 통과하면 x, β 및 γ 각도 x, y 및 z 축으로 O를, O를 기준으로 만듭니다.
- α, β 및 γ 각도는 선의 방향 각도라고하며,이 각도의 코사인은 방향 코사인을 제공합니다.
- 그림과 같이 보충 각도 β를 취할 수 있도록 방향 코스 사인에 대해 알 수있는 3 개의 장소에서 OQ를 연장한다고 가정 해 봅시다.
- 선의 방향을 되돌리면 방향 선이 반전됩니다.
- 포지션 벡터에 의한 각도와 양의 분기에서 라인의 방향을 고려한 후, 우리는 선 oq의 위치 벡터를 고려할 수 있습니다. .
OQ =Q라면
를 볼 수 있습니다x =QCOSα
y =QCOSβ
Z =QCOSγ
여기서 k는 벡터의 크기를 나타내고,
에 의해 주어집니다.Q =√ (x – 0) 2+ (y – 0) 2+ (Z – 0) 2
⇒q =x2+ y2+ z2
방향 각도의 코사인 cosα는 l
로 표시됩니다.방향 각도 cos β의 코사인은 m
로 표시됩니다.방향 각도의 코사인 Cosγ는 n
로 표시됩니다.x =qcosα =lq —————— (1)
y =QCOSβ =MQ ————— (2)
z =qcosγ =nq ————— (3)
직교 시스템을 사용하여 단위 벡터 구성 요소에서 Q를 나타낼 수도 있습니다.
q =xi + yj + zk
상기 식
에서 각각 LQ, MQ, NQ와 같이 X, Y 및 Z의 값을 대체합니다.Q =LQ I + MQ J + NQ Z
⇒r =qq =l i + m j + n z
- Q - 단위 벡터의 계수를 갖는 벡터의 방향 각도 코사인
- 단위 벡터 Q - 직사각형 구성 요소에 의해 해결됩니다
코사인 방향에 비례하는 숫자를 라인의 방향 비율이라고합니다. 선의 방향 비는 A, B, C
로 표시됩니다.또한 OQ2 =OA2+OB2+OC2
q =x2 + y2 + z2
방정식을 나누면 q =x2 + y2 + z2 우리는
를 얻는다.Q2Q2 =X2Q2+ Y2Q2+ Z2Q2
방정식 1,2,3
를 사용함으로써1 =xq2 + yq2 + zq2 =l2 + m2 + n2
위에서 언급 한 바와 같이, 방향 코사인의 제곱의 합. 1
A, B, C를 라인의 방향 비율로 두십시오
여기서 a∝l, b ,m, c∝n
그래서 우리는 a =kl, b =km, c =kn
를 얻습니다다음은 방향 비율과 라인의 방향 코사인 사이의 관계는 다음과 같습니다.
la =mb =nc =k
우리는 이미 l2 + m2 + n2 =1을 보았습니다.
K의 값은 지시 된 선의 방향에 따라 양수 또는 음수 일 수 있습니다
해결 된 예
좌표가있는 점 P (x, y, z)를 고려하십시오 (1, 2, 3). 질문의 주어진 값에 대해 원점 지점이 O (0, 0, 0) 인 직접 비율을 찾으십시오.
COS α, COSβ, COSγ =XR, YR, ZR
| r | =x2 + y2 + z2
| r | =12+ 22 + 32 =√14
우리는 COS α, COSβ, COSγ (Direction Cosines) =1√14,2√14, 3√14
를 결론 지었다주어진 지점 P (x, y, z)의 방향 비는 1 :2 :3입니다.
결론 :
방향 코사인은 3-D 평면에서 라인 방향을 나타내는 벡터입니다. 각도 라인이 x 축으로 만드는 경우 x 축이 y 축으로 β이고 z 축으로 γ이면 COS2α +COS2β +COS2γ =1. 방향의 방향을 나타내는 또 다른 방법입니다.