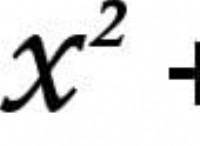에너지 밀도는 물리학의 다양한 가지에서 사용되는 개념입니다. 에너지는 화학, 전기 및 핵 물리학과 같은 다양한 시스템과 관련이 있으며 시스템의 에너지 함량에 대한 일반화 된 아이디어를 얻으려면 에너지 밀도의 개념이 적용됩니다. 천문학, 천체 물리학 및 우주론 분야에서 에너지 밀도에는 많은 응용이 있습니다. 에너지 밀도에 대한 치수 공식 의이 노트에서, 우리는 그 차원 공식에 대한 정의와 도출에 대해 논의합니다.
에너지 밀도의 치수 공식
에너지 밀도의 정의에서, 우리는 그것을 알고 있습니다
에너지 밀도 (e) =에너지/볼륨
따라서 에너지 밀도의 차원 =에너지의 차원 / 부피의 차원.
에너지의 치수 =작업의 차원 =힘의 차원 X 차원 변위
=[mlt-2]. [l] =[ml2t-2]
볼륨의 치수 =[l3]
에너지 밀도의 치수 =[ML2T-2]/[l3] =[ML-1T-2]
따라서 에너지 밀도의 차원은 [ML-1T-2]
입니다에너지 밀도의 의미
에너지 밀도는 단위 부피당 저장된 에너지의 양을 의미합니다. 단위 부피의 에너지의 양을 나타냅니다. 우리는 다른 시나리오에서 에너지 밀도를 측정합니다. 예를 들어, 핵 내부의 양성자와 중성자는 핵 결합 에너지라는 에너지에 의해 함께 유지된다. 에너지의 정확한 측정을 얻기 위해 에너지 밀도를 계산합니다. 에너지 밀도의 개념은 화학 반응 동안 동물에 의해 식품 및 산소에서 유래 한 에너지와 같은 다른 생물학적 계산에 유용합니다.
에너지 밀도는 자기 분야에서 중요한 역할을합니다. 에너지 밀도의 도움으로, 우리는 상호 및 자기 유도에 관한 다른 표현을 추론합니다.
에너지 밀도의 단위 :에너지 밀도를위한 SI베이스 단위는 kg/m.s2이지만 J/Lit W.H/Lit과 같은 다른 장치도 사용됩니다.
에너지 밀도는 우리가 크기에 대해서만 이야기 할 때 스칼라 양입니다. 방향이 관여하지 않습니다.
단위 및 측정의 치수
신체 금액의 치수 공식은 해당 금액으로 어떻게 보호되는지를 나타내는 표현으로 정의됩니다. 그것은 직사각형 괄호에서 적절한 강도, 즉 []를 갖는 기본 부분에 대한 기호를 둘러싸는 것을 통해 표시됩니다. 예는 질량의 치수 공식이며, 이는 (m)으로 제공됩니다. 중력으로 인한 가속도는 중력으로 인해 품목을 사용하는 데 도움이되는 가속도입니다. Si 장치는 m/s²입니다. 각각은 가치와 방향을 가지고 있습니다. 따라서 벡터 수량입니다. 중력으로 인한 가속도는 G를 사용하는 데 도움이됩니다. 지구의 일반적인 중력은 9.8m/s²로 주어집니다.
치수를 쓰는 예
사각형의 면적
사각형 영역의 공식을 취합시다
사각형의 면적 =길이 x 폭
=l x l (폭이 측면의 길이를 보여주는 곳)
=[l1] x [l1]
=[l2]
여기서 우리는 2의 힘까지의 길이를 볼 수 있으며 질량과 시간의 차원을 찾을 수 없습니다. 따라서 사각형 영역의 치수는 [M0 L2 T0]로 기록됩니다.
치수 공식
치수 공식은 전력과 함께 기본 물리적 수량을 가진 물리적 수량의 의존성을 나타냅니다.
예를 들어
속도의 공식
속도
의 공식을 취합시다속도 =거리 / 시간
거리는 길이로 쓸 수 있습니다 [l]
시간은 [t]
로 쓸 수 있습니다치수 공식은 [M0 L1 T-1]
입니다따라서 우리는 속도가 질량이 아닌 길이와 시간에만 의존한다고 결론을 내릴 수 있습니다.
치수 방정식
물리적 수량은 치수 방정식을 얻기 위해 치수 공식과 동일합니다.
예
속도 =[m0 l1 t-1].
치수 공식의 사용
치수 공식은 치수 방정식의 일관성과 일관성을 확인하는 데 도움이되는 도구가 될 수 있습니다. 치수 공식은 또한 물리적 현상의 물리적 양 사이의 상관 관계를 확립하는 데 사용될 수 있습니다. 이 공식은 단위를 한 시스템에서 다른 시스템으로 변경하는 데 사용될 수도 있습니다.
치수 분석의 적용
실제 물리학에서 치수 분석은 측정의 중요한 부분입니다. 우리는 다음과 같은 이유로 치수 분석을 사용합니다.
- 치수 방정식이 일관되도록하기 위해;
- 물리적 현상에서 물리적 수량 간의 관계 결정;
- 한 장치에서 다른 장치로 전환하려면
치수 공식의 한계
치수 공식은 치수 상수와 관련이 없습니다. 또한, 삼각법, 지수, 로그 등과 같은 함수를 포함하는 모든 공식은 도출 될 수 없습니다. 물리적 수량이 스칼라 또는 벡터라는 맥락에서, 수량이 물리적인지 아닌지에 대한 정보를 제공하지 않습니다.
결론
에너지 밀도의 차원 공식에 대한이 장에서, 우리는 에너지 밀도의 기초와 그 차원 분석을 배웠습니다. 우리는 또한 다른 사용 사례와 에너지 밀도를 사용한 이유를 배웠습니다. 상당히 큰 시스템을 다룰 때는 정확한 에너지 밀도를 결정할 수 없습니다. 계산을보다 정확하게하기 위해 에너지 밀도를 도출합니다.