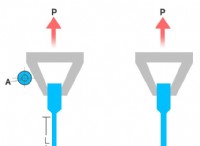
설정 이해
* 공 : 수직으로 매달려있는 질량 'm'.
* 문자열 : 공을 풀리에 연결하는 가벼운 끈은 질량이없고 성체가 불가능하다고 가정합니다.
* 풀리 : 관성 모멘트 (I) 및 반경 (R)을 갖는 균일 한 솔리드 디스크.
* 마찰없는 액슬 : 풀리는 마찰 손실없이 자유롭게 회전합니다.
주요 개념
* 에너지 보존 : 시스템의 총 기계적 에너지 (볼 및 풀리)는 일정하게 유지됩니다. 이것은 잠재적 에너지의 합계, 공의 운동 에너지 및 풀리의 회전 운동 에너지가 일정하다는 것을 의미합니다.
* 회전 운동 : 풀리는 현의 장력에 의해 생성 된 토크로 인해 각속 가속을 경험합니다.
* 토크 : 문자열의 장력은 풀리에 토크를 생성하여 회전하게합니다.
* 관성의 순간 : 대상이 회전 운동의 변화에 얼마나 강한 지에 대한 척도. 솔리드 디스크의 경우 i =(1/2) MR².
방정식 도출
1. 공에 작용하는 힘 :
* 중력 :MG (아래쪽)
* 문자열의 장력 :t (위쪽)
2. 풀리에서 작용하는 힘 :
* 문자열의 장력 :t (접선 힘)
3. 공을위한 움직임 방정식 :
* Newton의 두 번째 법칙 :Ma =mg -t
* 공의 가속도 :a =(g -t/m)
4. 풀리의 움직임 방정식 :
* 토크 :τ =tr
* 각 가속도 :α =τ/i =(tr)/(1/2mr²) =(2T/MR)
* 선형 가속도 (a)와 각속도 (α)의 관계 :a =rα
5. 에너지 보존 :
* 공의 초기 잠재적 에너지 :MGH (여기서 'H'는 초기 높이)
* 공의 최종 잠재 에너지 :0 (공이 바닥에 도달 할 때)
* 공의 운동 에너지 :(1/2) mv²
* 풀리의 회전 운동 에너지 :(1/2) iω² =(1/4) Mr²ω²
6. 선형 및 각속 속도 관련 :
* V =RΩ
문제 해결
1. 장력을 해결합니다 (t) :
* 볼의 운동 방정식에서 'A'에 대한 표현을 선형 및 각속도 (A =Rα) 사이의 관계로 대체하십시오.
* t =(2/3) mg을 찾을 수 있습니다
2. 가속도를 찾으십시오 (a) :
* t 값을 볼의 운동 방정식으로 대체하십시오 (ma =mg -t).
* 당신은 a =(1/3) g를 얻을 수 있습니다
3. 각도 가속도 (α) :
* 방정식 α =(2T/MR)를 사용하고 T의 값을 대체하십시오.
4. 볼의 속도 (v)를 결정하십시오 :
* 에너지 방정식의 보존을 사용하고 'V'를 해결하십시오.
키 포인트
* 문자열의 장력은 풀리의 회전 관성으로 인해 공의 무게보다 작습니다.
* 풀리의 회전이 느려지기 때문에 볼의 가속도는 'G'보다 작습니다.
* 공이 떨어지면서 손실 된 에너지는 풀리의 회전 운동 에너지로 전달됩니다.
특정 질문이 있거나 이러한 값을 계산하려는 경우 알려주십시오. 필요한 경우 더 자세한 계산을 제공 할 수 있습니다.