정상 상태 근사치

핵심 개념

이 기사에서는 연속 반응의 동역학을 이해하는 데 중요한 도구 인 정상 상태 근사치에 대해 배우게됩니다.

정상 상태 근사가없는 연속 반응 동역학

정상 상태 근사치는 수학 모델링 연속 반응 메커니즘을 단순화하는 유용한 도구입니다. 화학 동역학에서, 연속 반응은 간단한 동역학을 가질 수 있지만 종종 두통을 유발하는 수학을 포함합니다. 다음과 같은 연속 반응을보십시오 :

A → B → C

분자 A는 B로 변환되며, 이로 인해 C. 속도 상수 k _a 로 변환됩니다. 및 k _b 첫 번째 및 두 번째 반응의 속도를 각각 알립니다. 각 반응은 분자 단백질이므로 반응에서 각 종의 변화율을 쉽게 찾을 수 있습니다.

-k _a [a] =(d [a])/t

k _a [a] -k _b [b] =(d [b])/t

(d [c])/t =k _b [b]

1 차 요율 법칙을 사용하여 시간이 지남에 따라 A의 농도를 모델링하는 방정식을 찾을 수 있습니다.

[a] =[a] ₀ e

그런 다음이 요금 법을 B :

(d [b])/t+k _b [b] =k _a [a] 0 e

B의 초기 농도가 없다고 가정하면이 미분 방정식을 해결할 수 있습니다. =0) 그리고 그 k _a ≠ k _b :

[b] =(e-e) k _a /(k _a -k _b )

마지막으로, 우리가 또한 C ([c] ₀ 의 초기 농도가 없다고 가정하면 =0, [a] + [b] + [c] =[a] ₀ ), 우리는 시간이 지남에 따라 C의 농도에 대한 방정식을 얻습니다.

[c] =[a] 0 (1+ (k _a e-k _b e)/(k _b -k _a )))

보시다시피, 1 차 동역학의 상당히 간단한 개념을 사용하면 연속 반응을위한 수학은 복잡해집니다. 두 단계 이상의 반응을 고려하면 수학은 관리 할 수 ​​없습니다. 이것은 정상 상태 근사치가 유용한 곳입니다.

비 분자 동역학에 대한 정상 상태 근사치

정상 상태 근사치는 중간 화합물 인 분자 B의 농도의 변화가 항상 무시할 수없는 경우에도 항상 매우 낮게 유지된다고 주장한다.

(d [b])/t ≈ 0

이 근사치를 만들기 위해 연속 반응 시스템은 두 가지 종종 진실한 기준을 충족해야합니다.

• B의 농도는 일반적으로 A 또는 C에 비해 훨씬 낮습니다.
• 형태 B에 반응하는 A의 비율은 B 형태 C에 반응하는 B의 속도보다 훨씬 느립니다. 이것은 형성 B가 속도 결정 단계입니다.
.

많은 연속 반응 시스템이 이러한 기준을 충족합니다. 종종 B는 불안정한 중간체로 작동하여 특정 낮은 임계 값을 충족 할 때까지 처음에는 농도가 상승하게됩니다. 그런 다음 생성 된 추가 B는 불안정성으로 인해 B의 생산보다 훨씬 빠르게 C로 빠르게 변환됩니다. 수학적으로 이것은 KB가 KA보다 훨씬 많은 양을 나타낸다는 것을 의미합니다.

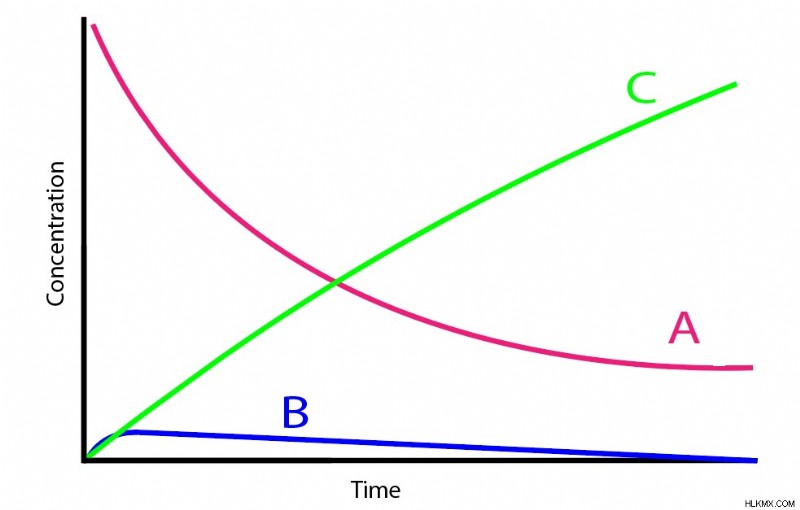
두 기준이 모두 충족되면 정상 상태 근사치가 수학을 크게 단순화합니다. 즉, A와 B의 농도를 직접 관련시키는 방법을 제공합니다.

0 =(d [b])/t =k _a [A] - K _B [b]

(k _a /k _b ) [a] =[b]

이것은 우리가 시간의 함수로서 C의 농도에 대한 표현에 더 쉽게 도달 할 수있게한다 :

[a] 0 =[a] + [b] + [c]

[c] =[a] 0 - [a] - [b]

[c] =[a] 0 - [a] - (k _a /k _b ) [a]

그런 다음 시간 측면에서 C를 변경하기 위해 A의 변경과 관련된 1 차 요율 법을 구현합니다.

[c] =[a] 0 - ([a] ₀ e) - ((k _a /k _b ) [a] ₀ e)

[c] =[a] 0 (1 - E - (k _a /k _b ) e)

종종 k _a 인 경우 방정식을 더 단순화 할 수 있습니다 k _b 에 비해 무시할 수 있습니다 (k _a /k _b ≈ 0). 이것은 우리가 괄호에서 세 번째 용어를 무시하고 다음을 산출 할 수있게합니다.

[c] =[a] 0 (1 - E)

효소 동역학에 대한 정상 상태 근사치

불일치 동역학 외에도, 정상 상태 근사치는보다 복잡한 연속 반응에서 유용하다는 것을 입증합니다. 비 분자 반응에서 근사치의 가장 중요한 적용은 효소 촉매의 Michaelis-Menten 동역학을 포함한다. 일반적인 효소-촉매 반응에서, 기질 (S)은 효소 (E)에 가역적으로 결합하여 효소--하류 복합체 (ES)를 형성한다. 그런 다음, 효소는 복합체로부터 방출되는 생성물 (P)의 형성을 촉매한다 :

e + s es → e + p

이전의 단 분자 반응과 달리,이 반응은 3 개의 총 속도 상수를 포함합니다. k ₁ 복합체를 형성하는 효소 및 기질의 순방향 속도를 설명하고, K _-1 . 역 반응을 설명합니다. k ₂ 생성물의 형성 및 복합체로부터 효소의 재생과 관련이있다. 수학을 단순화하기 위해, 우리는 종종 정상 상태 근사와 평형과 관련된 또 다른 유용한 근사치를 구현할 수 있습니다.

정상 상태가 효소에 어떻게 적합한 지

생물학적 시스템과 산업 응용 분야에서, 기질은 광대 한 효소에 존재하는 경향이있다. 낮은 효소 농도는 복합체의 형성을 제한하기 때문에“중간 농도의 낮은 농도”조건을 충족시킨다. 고농도의 기질은 본질적으로 모든 효소가 기질로 포화되어야하기 때문에 효소 복합체의 정상 상태를 가정 할 수 있습니다. 이것은 반응 기간 동안 일정하게 남아있는 효소-하류 복합체의 농도를 초래한다 :

(d [es])/t =0

단순화 된 수학

복합체의 농도 변화를 표현하기 위해, 우리는 첫 번째 반응의 순방향 속도를 역전 속도와 두 번째 반응의 순방향 속도를 사용한다. 중요하게도, 우리는 1 차 및 2 차 요율 법을 사용하여 이러한 각 요금을 도출 할 수 있습니다. 그런 다음 정상 상태 근사치를 사용하여 세 가지 요금을 연관시킬 수 있습니다.

(d [es])/t =0 =k ₁ [E] [S]-K _-1 [es] - K ₂ [es]

k ₁ [E] [s] =k _-1 [es] + k ₂ [es]

그런 다음 다음 방정식을 생성하기 위해 재 배열 할 수 있습니다.

([e] [s])/([es]) =(k _-1 + k ₂ )/k ₁

이 시점에서, 우리는 [e]와 [es]가 수학적으로 서로 관련이 있음을 기억해야합니다. 구체적으로, 그들의 첨가는 사용 및 사용하지 않는 효소의 총 농도를 산출합니다.

[e] _총 =[e] + [es]