수학에서, 함수의 점근선은 함수가 무한하게 가까워 지지만 결코 도달하지 않는 줄입니다. 보다 정확한 수학적 용어로, 곡선의 점근선은 라인으로 정의되어 선과 곡선 사이의 거리가 곡선의 x 및 y 좌표 중 하나 또는 둘 다로 인한 경향이 있기 때문에 라인과 곡선 사이의 거리가 0에 접근하도록 라인으로 정의 될 수있다. 다시 말해, 점근선은 기능이 영원히 가까워 지지만 실제로 도달하지 않는 그래프의 선입니다.
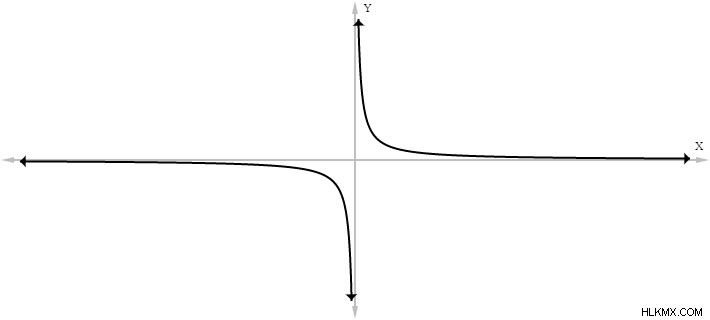
세 가지 주요 종류의 무증상이 있습니다. 수직, 수평 및 경사; 각각 좌표 평면에 대한 방향을 기준으로 정의됩니다. 수직 점근선은 가장 흔하고 가장 쉬운 점근선입니다. 수직 점근선은 정의되지 않은 경사가있는 선과 같습니다. 요컨대, 합리적 함수의 수직 점근선은 그 합리적 함수의 분모를 0으로 설정하는 X 값에 위치합니다. 합리적 함수는 두 개의 다항식 방정식의 몫으로 표현되는 함수입니다. 예를 들어, 합리적 함수의 그래프 ƒ ( x ) =1/ x ² :
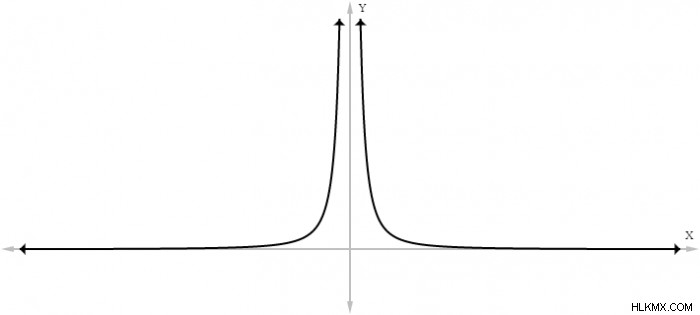
x를 0과 동일하게 설정하면 합리적 함수에서 분모를 설정합니다 ( x ) =1/ x ² ~ 0. 따라서이 함수는 x =0 라인에 위치한 수직 점근선이 있습니다. 수직 점근선은 단일 그래프에 다수의 수직 점근을 가질 수 있다는 점에서 독특합니다. 반대로, 그래프는 최대 하나의 수평 또는 하나의 비스듬한 점근선을 가질 수 있습니다.
점근선의 개념
처음에, 점근선의 개념은 우리의 일상적인 경험에 반하는 것 같습니다. 컴퓨터 화면의 종이 조각 또는 픽셀의 선과 같은 그래프의 곡선의 물리적 표현은 유한 한 너비를 가지고 있습니다. 이 라인을 충분히 확장함으로써, 곡선은 결국 점근선을 만나거나 적어도 우리의 비전이 말할 수있는 한, 적어도 우리의 비전이 말할 수있는 한 것 같습니다. 그래프는 이상적인 수학적 실체의 물리적 표현이라는 점을 명심해야합니다. 이상화 된 기하학적 선은 폭이 0이므로 수학 라인은 실제로 그것과 일치하지 않고도 영원히 더 가까워 질 수 있습니다.
어떤면에서,“일부 수량에 접근하지만 결코 도달하지 않는 가치”라는 개념은 변화, 운동 및 연속성에 관한 고대 그리스 역설에서 그 기원을 찾는 것으로 간주 될 수 있습니다. Elea의 Zeno가 제공 한 유명한 예는 다음과 같습니다. Great Athlete Achilles는 100 미터 대시를 운영하고 있습니다. 100 미터를 달리려면 먼저 거리의 절반을 덮어야하므로 50 미터를 달리려면됩니다. 나머지 50 미터를 달리려면 먼저 그 거리의 절반, 따라서 25 미터를 덮어야합니다. 나머지 25 미터를 덮으려면 먼저 그 거리의 절반을 커버해야하므로 12.5 미터입니다. 나머지 12.5 미터를 건너려면 먼저 그 거리의 절반을 건너야합니다.
이 추론 ad infinitum 를 추정합니다 아킬레스가 절대 절대 가하지 않을 것이라는 반 직관적 인 결론으로 이어집니다 결승선을 건너십시오. 항상 가 있습니다 그가 먼저 건너야하는 유한 한 거리가되므로 실제로 결승선에 도달하지 않을 것입니다. 철학자들과 수학자들은 수세기 동안 제노의 역설에 의아해했다. Zeno에게 알려지지 않은 그의 역설의 역설은 현대의 수학적 점근자의 개념을 포착하는 데 매우 가깝습니다.
수직 점근선의 정의
점근선의 첫 번째 공식 정의는 미적분학의 한계 개념과 함께 발생했습니다. 함수의 한계는 함수가 매개 변수 중 하나가 무한대로 접근하는 값입니다. 따라서 함수는 해당 값의 방정식 제한이 무한대가되도록 일부 값으로 점근선을 가지고 있습니다.
우리는 수직 점근선을 결정하기가 가장 일반적이며 가장 쉽기 때문에 수직 무증상 만 고려할 것입니다. 기능에 수직 점근선이 있는지 확인하기위한 일반적인 조건은 다음과 같습니다. 함수 ƒ (x)는 x =a가있는 경우에만 x =a가 x 접근으로 바인딩되지 않은 경우에만 수직 점근선을 갖습니다. a . 즉, 함수는 x =a가있는 경우에만 수직 점근선이 있습니다. 무한대와 같습니다.
마지막 단락은 입이 많았 으므로이 아이디어를 살리기위한 간단한 예를 살펴 보겠습니다. 다음은 함수의 그래프 ƒ (x) =1/x입니다. 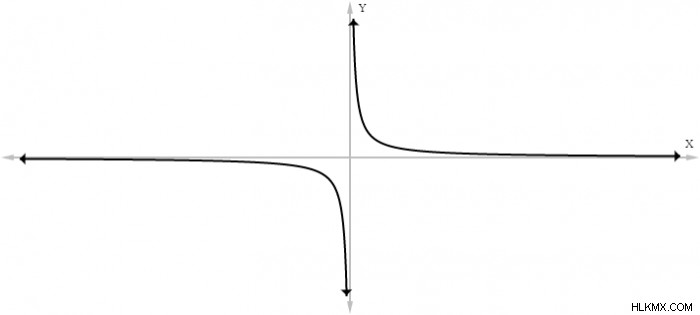
이 함수는 역 곡선의 형태를 취합니다. x의 값이 양쪽에서 0에 접근하기 때문에 함수의 동작에 주목하십시오. x 값이 0에 가까워지면서, 긍정적 인 방향과 부정적인 방향으로 결합하지 않고도 기능이 빠르게 성장하기 시작합니다. 기능에 0에 가까워지는 X 값을 막기 시작할 때 어떤 일이 발생하는지 보자.
ƒ (1) =1/1 =1
ƒ (0.5) =1/0.5 =2
ƒ (0.25) =1/0.25 =4
ƒ (0.1) =1/0.1 =10
ƒ (0.01) =1/0.01 =100
ƒ (0.001) =1/0.001 =1000
ƒ (0.000001) =1/0.000001 =1,000,000
ƒ (0.00000001) =1/0.00000001 =100,000,000
x가 0에 접근함에 따라, 함수의 출력은 무한대에 대한 양의 방향으로 임의로 크게됩니다. 가장 중요한 것은 ƒ (0)에 대해 함수가 정의되지 않기 때문에 함수는 x =0에서 선을 교차하지 않습니다 (1/0은 정상적인 산술에서 정의되지 않음). 마찬가지로 왼쪽에서 0에 접근하면 값이
입니다.ƒ (-0.5) =1/-0.5 =-2
ƒ (-0.25) =1/-0.25 =-4
ƒ (-0.1) =1/-0.1 =-10
ƒ (-0.01) =1/-0.01 =-100
ƒ (-0.001) =1/-0.001 =-1000
ƒ (-0.000001) =1/-0.000001 =-1,000,000
ƒ (-0.00000001) =1/-0.00000001 =-100,000,000
X가 왼쪽에서 0에 접근함에 따라, 함수의 출력은 음의 무한대에 대한 음의 방향으로 임의로 크게 증가한다. 기능은 어느 쪽이든 점근선에 접근 할 때 어느 방향 으로든 임의로 커지기 때문에 이중 측면 점근선입니다. 일부 기능은 한쪽에서 단위로 만 접근합니다.
수직 점근을 찾는 방법
합리적인 기능의 수직 점근선을 찾는 것은 비교적 간단합니다. 합리적 함수의 분모를 0으로 설정하는 x 값을 찾는 것입니다. 간단한 예는 다음과 같습니다.
함수의 수직 점근선 얼마나 ƒ (x) =(x+4)/3 (x-3)?
이것은 간단합니다. 우리가해야 할 일은 분모 제 3 (x-3)을 0과 동일하게 만드는 X 값을 찾는 것입니다. 순간의 관찰에 따르면 대답이 x =임을 알려줍니다. 3 ; 함수 ƒ (x) =(x+4)/3 (x-3)은 x =3에서 수직 점근선이 있습니다.
직접 계산 대신, 합리적 기능을 그래프로 그래프로 그래프가 해당 함수가 점근이 있는지 여부를 결정하는 데 도움이 될 수 있습니다. 함수에 대한 그래프 ƒ (x) =(x+4)/(x-3)은 다음과 같습니다. 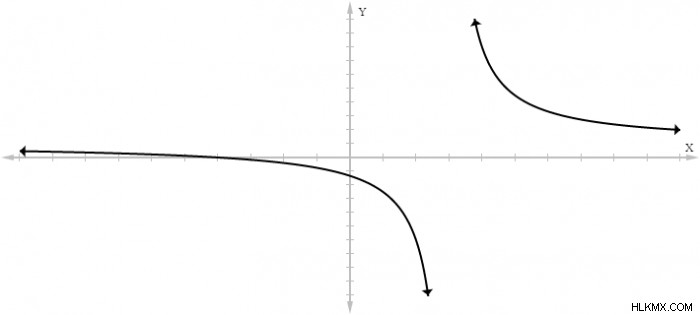
X가 왼쪽과 오른쪽에서 3에 접근하는 방법에 주목하십시오. 함수는 각각 음의 무한대와 양의 무한대에 결합하지 않고 성장합니다. 그래프를 보는 것만으로도 함수가 수직 점근선이 있다는 증거는 아니지만 찾을 때 시작하는 데 유용한 장소가 될 수 있습니다.
솔루션에 대한 더 많은 문제
수직 무증상을 찾는 데 익숙해지기 위해 몇 가지 문제를 살펴 보겠습니다.
(1)
함수의 수직 점근선 ƒ (x) =(x+2)/(x²+2x -8)?
솔루션 :
다시 한 번, 분모 용어를 0과 동일하게 설정하는 x 값을 찾아야합니다.이 경우 분모 용어는 (x²+2x -8)입니다. 이 용어를 고려하여 0으로 설정하는 x 값을 찾을 수 있습니다. 팩터링 (x²+2x -8)은 우리에게 다음과 같습니다.
(x²+2x-8) =(x+4) (x-2)
이 함수는 실제로 분모 항을 0, x =-4 및 x =2에 해당하는 2 x 값을 갖습니다. 따라서 함수 ƒ (x) =(x+2)/(x²+2x -8)에는 -4 및 2에서 2 개의 점근선이 있습니다.이 방정식을 그래프로 표시합니다. 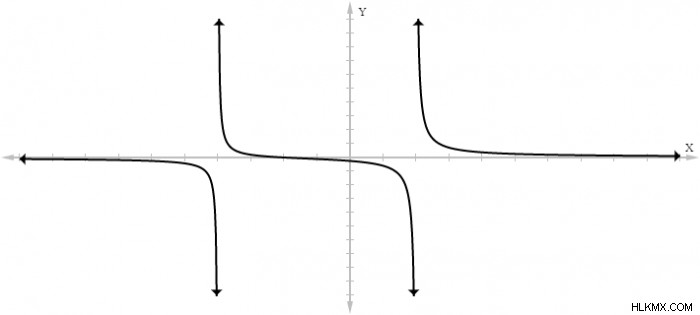
방정식을 그래프로 만들면이 함수에 x 값 -4 및 2에 위치한 2 개의 수직 무증상이 있음을 알 수 있습니다.
(2)
함수의 점근선은 무엇입니까? (x) =(x³ -8)/(x²+9)?
솔루션 :
이것을 알아 내려면 분모를 0으로 설정해야하므로 :
x²+9 =0
x² =-9
멍청이! 이 방정식에는 해결책이 없습니다. 숫자 제곱은 항상 0보다 크기 때문에 x²가 -9와 같아 X의 값이 없습니다. 따라서 분모를 0으로 설정할 수있는 x 값은 없으므로 함수 ƒ (x) =(x+2)/(x²+2x -8)에는 수직 점근선이 없습니다!
.(3)
함수의 점근선 (S)은 무엇입니까? (x) =x/(x²+5x+6)?
솔루션 :
다시 한 번, 분모 용어를 고려하여 항을 0으로 설정하는 x 값을 찾아서이 값을 해결할 수 있습니다. 하부 항 x²+5x+6을 고려합니다.
.x²+5x+6 =(x+2) (x+3)
이 다항식에는 0, x =-2 및 x =-3에 해당하는 두 가지 값이 있습니다. 따라서 함수 ƒ (x) =x/(x²+5x+6)는 x =-2 및 x =-3에서 2 개의 수직 무증상을 갖습니다. 이 기능을 그래프로 표시하면 다음과 같습니다. 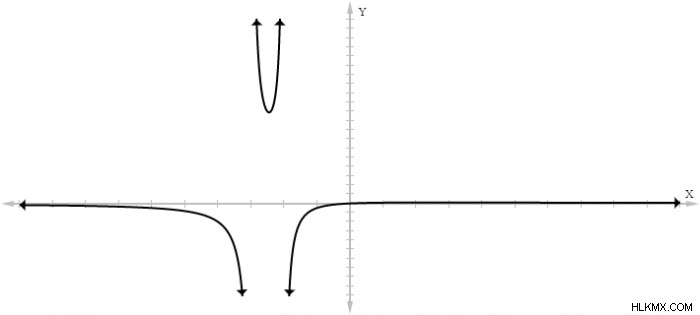
이 그래프가 왼쪽에서 -3, 오른쪽에서 -2에 접근함에 따라 함수는 음의 무한대에 접근합니다. 오른쪽에서 -3, 왼쪽에서 -2에 접근함에 따라 함수는 무한대에 묶이지 않고 자랍니다. 이 두 점근의 배치는 그래프를 세 개의 별개의 부분으로 자릅니다.
요약하면, 수직 점근선은 기능의 매개 변수 중 하나가 무한대 경향이있는 일부 함수가 접근하는 수직선입니다. 함수는 영원히 가까워지고 점근선 BU가 실제로 만지지 않을 것입니다. x =a가있는 경우에만 함수는 수직 점근선이 있습니다. 분모 용어를 0으로 설정하는 x 값을 찾아서 합리적 기능의 수직 무증상을 결정할 수 있습니다.