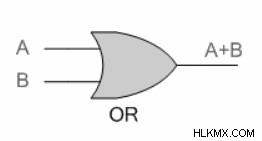
19 세기 영국 수학자 인 Augustus de Morgan이 제공 한 두 가지 법률은 De Morgan의 정리라고합니다. 두 법률은 규칙을 사용하거나, 그렇지 않은 기능을 사용합니다. 이들 함수의 특성을 사용하면 한 부울 표현식이 한 형태에서 다른 형태로 변환 될 수있다. 첫 번째 정리는 제품의 역전이 반전의 합과 동일하다고 명시하고 있습니다. 두 번째 정리는 합의 역전이 반전의 산물과 동일하다고 말합니다. De Morgan의 정리는 둘 이상의 변수에 대해 사실입니다.
첫 번째 정리
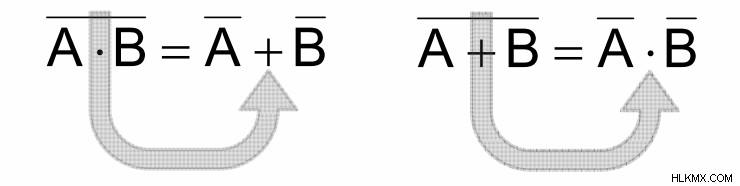
De Morgan이 제공 한 첫 번째 정리에 따르면, 둘 이상의 변수가 있고 보완 될 때, 이는 각 변수의 보완 물과 개별적으로 동일합니다. 첫 번째 De Morgan 정리는 다음과 같이 쓸 수 있습니다.

진실 테이블을 사용하여 첫 번째 De Morgan의 정리 확인

첫 번째 정리의 구현
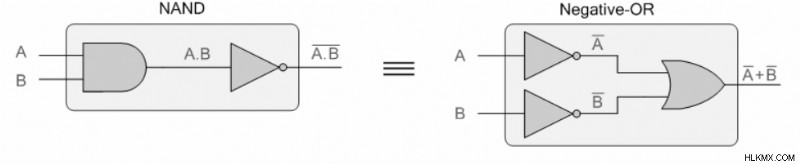
제 1 정리의 증거

 두 번째 정리
두 번째 정리
De Morgan이 제공 한 두 번째 정리에 따르면, 둘 이상의 변수가 또는 보완 될 때, 이는 각 변수의 보완 및 개별적으로 상보하는 것과 동일합니다. 두 번째 De Morgan 정리는 다음과 같이 쓸 수 있습니다.

진실 테이블을 사용하여 첫 번째 DE Morgan 정리 확인

두 번째 정리의 구현
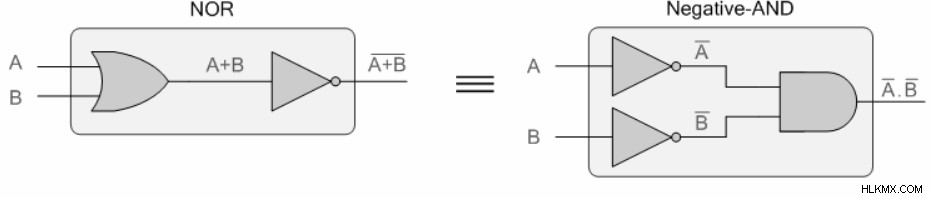
두 번째 정리의 증거


단순화
de Morgan 정리를 사용하여 표현식을 단순화하려면 다음 단계를 사용하십시오.
-
‘또는’를‘및’및‘및’로‘또는’로 대체합니다. 다시 말해서,‘+’를‘⋅’,‘⋅’로 바꾸십시오.
-
표현식
에서 각 항을 보완합니다
예제 1

예제 2
동등한 게이트
de Morgan의 정리를 사용하여 동등한 게이트를 얻으려면 게이트를 또는 게이트로 교체하십시오. 또한 게이트의 모든 입력과 출력을 반전시킵니다. De Morgan 's 정리의 몇 가지 예를 살펴 보겠습니다.
예제 1
다음과 같이 기본과 게이트를 가져 가자 :
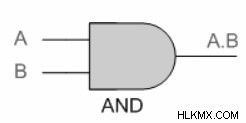
동등한 게이트를 찾으려면 게이트를 또는 게이트로 교체하고 두 개의 입력과 하나의 출력을 다음과 같이 사용하지 않습니다.
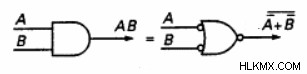
(입력 및 출력의 기포는 반전을 나타냅니다.)
위의 표현이 다음과 같이 진실 테이블을 사용하여 동등한 지 확인해 봅시다 :
예제 2
다음과 같이 기본 또는 게이트를 가져 가자 :
동등한 게이트를 찾으려면 OR 게이트를 교체하고 게이트를 교체하고 다음과 같이 게이트를 사용하여 두 입력과 하나의 출력을 반전합니다.
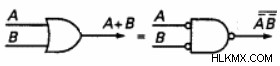
(입력 및 출력의 기포는 반전을 나타냅니다)
위의 표현이 다음과 같이 진실 테이블을 사용하여 동등한 지 확인해 봅시다 :