1. 정확한 언어 :
* 현실 정량화 : 물리학은 거리, 시간, 질량, 힘 등과 같은 측정 가능한 양을 다룹니다. 수학은 이러한 수량을 정확하고 객관적으로 표현하는 도구 (숫자, 방정식, 미적분학)를 제공합니다.
* 모호성 제거 : 단어는 모호 할 수 있지만 수학적 기호는 잘 정의 된 의미를 가지고 있습니다. 이를 통해 물리학 자들은 자신의 아이디어를 모호하게 전달하고 서로의 작업을 쌓을 수 있습니다.
2. 모델링 및 예측 :
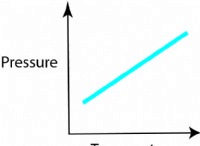
* 현상을 나타내는 : 수학적 모델은 물리적 현상을 나타내는 데 사용됩니다. 이 모델은 방정식, 그래프 또는 복잡한 컴퓨터 시뮬레이션 일 수 있습니다.
* 테스트 이론 : 물리학 자들은 수학적 모델의 예측을 실제 관찰과 비교함으로써 이론의 유효성을 테스트 할 수 있습니다.
* 예측 : 모델이 검증되면 미래의 사건이나 현상에 대한 예측에 사용될 수 있습니다.
3. 패턴과 관계 발견 :
* 숨겨진 연결 공개 : 수학은 겉보기에는 관련이없는 물리적 수량 사이의 패턴과 관계를 보여줍니다. 예를 들어, 뉴턴의 보편적 중력 법칙은 물체의 질량과 그들 사이의 중력의 힘 사이의 관계를 설명합니다.
* 복잡성 단순화 : 미적분학과 같은 수학적 도구를 사용하면 물리학자가 복잡한 현상을 더 간단하고 관리하기 쉬운 부분으로 분해 할 수 있습니다.
4. 추상 추론 :
* 관찰 가능한 것 이상 : 물리학의 많은 기본 개념 (양자 역학과 같은)은 매우 추상적입니다. 수학은 이러한 추상 아이디어를 추론하고 이해하기위한 프레임 워크를 제공합니다.
* 개념 재단 : 벡터, 텐서 및 미분 방정식과 같은 수학적 구조는 많은 현대 물리 이론의 기초를 형성합니다.
물리학 수학의 예 :
* 뉴턴의 운동 법칙 : 미분 방정식을 사용하여 설명했습니다.
* Maxwell의 방정식 : 벡터 및 미적분학을 사용한 전자기를 나타냅니다.
* 아인슈타인의 상대성 이론 : 텐서 및 형상과 같은 고급 수학 개념을 사용합니다.
* 양자 역학 : 파동 함수 및 연산자와 같은 복잡한 수학 구조를 기반으로합니다.
결론 :
수학은 도구 일뿐 만 아니라 우주를 이해하기위한 필수 언어와 틀입니다. 물리학 자들은 비교할 수없는 정밀도와 엄격한 물리적 현상을 설명, 예측 및 분석 할 수 있습니다. 수학과 물리학 사이의 친밀한 관계는 세상에 대한 우리의 이해에서 놀라운 발전을 이끌어 냈으며 미래의 발견에 계속 필수적입니다.