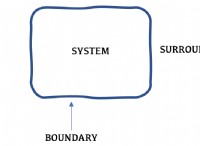
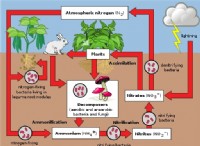
* 회전 축 : 관성 모멘트는 나선이 자체 축을 중심으로 회전하는지 여부에 따라 다릅니다.
* 질량 분포 : 나선에 균일 한 질량 밀도가 있으면 계산이 더 간단 해집니다. 질량이 불균일 한 경우 통합이 필요합니다.
나선의 관성 순간을 계산하는 일반적인 접근법은 다음과 같습니다.
1. 나선 정의 :
- 나선을 파라 메트릭 방정식으로 정의하도록하십시오.
* x =r* cos (t)
* y =r* sin (t)
* z =b* t
여기서 'r'은 나선의 반경 인 'b'는 피치 (연속 회전 사이의 수직 거리)이고 't'는 매개 변수입니다.
2. 회전 축 : 나선이 회전하는 축을 지정하십시오.
3. 나선을 작은 요소로 나눕니다. 나선을 각각 질량 'DM'으로 무한 질량 요소로 나누는 것을 상상해보십시오.
4. 각 요소의 관성 모멘트를 계산하십시오 : 선택한 축에 대한 단일 요소의 관성 모멘트는 다음과 같이 제공됩니다.
-i =dm * r^2
여기서 'r'은 요소에서 회전 축까지의 수직 거리입니다.
5. 전체 나선에 통합 : 나선의 전체 길이에 DI를 통합하여 모든 무한 요소의 관성 모멘트를 요약하십시오.
6. 질량 분포를 고려하십시오 : 나선에 균일 한 질량 밀도가 있으면 'DM'은 요소 길이의 함수로 표현 될 수 있습니다. 밀도가 불균일 한 경우 통합에서 고려해야합니다.
예 :자체 축 주위의 나선의 관성 순간 :
균일 한 질량 밀도 'ρ'와 길이 'l'가있는 나선을 고려해 봅시다.
* 파라 메트릭 방정식 : x =r*cos (t), y =r*sin (t), z =b*t.
* 회전 축 : 나선의 축.
* 질량 요소 : dm =ρ * ds, 여기서 ds는 무한 요소의 아크 길이입니다.
* 수직 거리 : r =r (요소는 이미 축에서 'r'거리에 있기 때문에).
* 통합 :
- 우리는 나선 길이에 di =dm * r^2 =ρ * ds * r^2를 통합해야합니다.
- 아크 길이 ds는 ds =sqrt (dx^2 + dy^2 + dz^2) =sqrt (r^2 + b^2) * dt로 표현할 수 있습니다.
- 통합 한계는 0에서 l/(b*sqrt (r^2 + b^2))입니다.
최종 결과는 'ρ', 'r', 'b'및 'l'을 포함하는 필수적인 표현이 될 것입니다.
참고 : 특정 회전 축과 질량 분포에 따라 계산이 상당히 복잡해질 수 있습니다. 고급 통합 기술이 필요할 수 있으며 타원 적분이 포함될 수 있습니다. 특정 나선에 대한 특정 계산이 필요한 경우 나선 및 회전 축에 대한 세부 정보를 제공하면보다 정확한 솔루션을 제공하는 데 도움이됩니다.